MESOSCALE & CONTINUUM MODELING

Mesoscale & Continuum Modelling

ABOUT R&D ACTIVITIES R&D PROGRAMS PUBLICATIONS PEOPLE CONTACT US

ABOUT

The research of Modelling and Mechanics group aims to the investigation of new problems in mechanics of materials, optics, and quantum mechanics and its applications in nanosciences, mathematical biology and mathematical geophysics. The main focus of the group is in the continuum modelling of discrete atomistic problems, the constitutive modelling of graphene and germanium, the dynamics of optical waves in photonics graphene and lattices, the dynamic behaviour of magnetic materials and skyrmionic textures, and in the semiclassical modelling of acoustic and elastic waves and quantum systems. The group develops novel models, new analytical methods and numerical techniques, and contributes to the training of graduate students and young researchers, with diverse background in physics, applied mathematics and engineering, working on these problems from different perspectives.

RESEARCH AND DEVELOPMENT ACTIVITIES

Continuum Modelling of Discrete Atomistic Problems: Research on this field aims to the development of various techniques from discrete mathematics to provide exact connections of continuum and atomistic descriptions of crystalline solids, such as nanoparticles. We have developed a new concept of lattice-cell average that allows such connections. We are able to provide explicit exact expressions for surface and edge energies of nanocrystals, for general interatomic potentials, and a new expression of the interfacial energy of deformation twins and phase boundaries, with extensions beyond pairwise interactions.

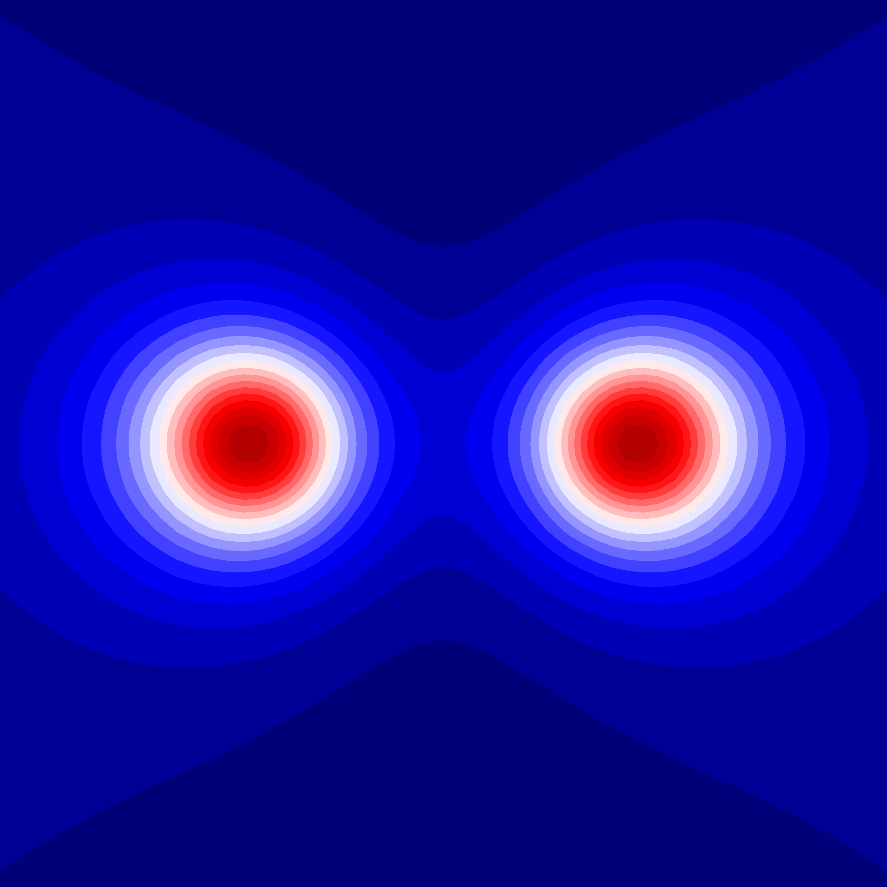
Constitutive continuum modelling of monoatomic and diatomic multilattices: Research in this area employs the arithmetic symmetry group to model materials used in emerging technologies, such as graphene, germanium, hexagonal boron nitride and others, in the discrete level. Confinement to weak transformation neighbourhoods and use of the Cauchy-Born rule allow for the transition from the discrete to the continuum description, where someone is able to work with the geometric symmetry group. The theory of invariants is used to build up generic expressions for the energy that fully capture material’s anisotropy at the continuum level both for the small and finite deformation regime. When there is no available representation theory one may use the theory of integrity basis to build the energy functions. Such energies describe in the most general way the mechanical response of materials at the microscale when they are scaled up to the continuum.

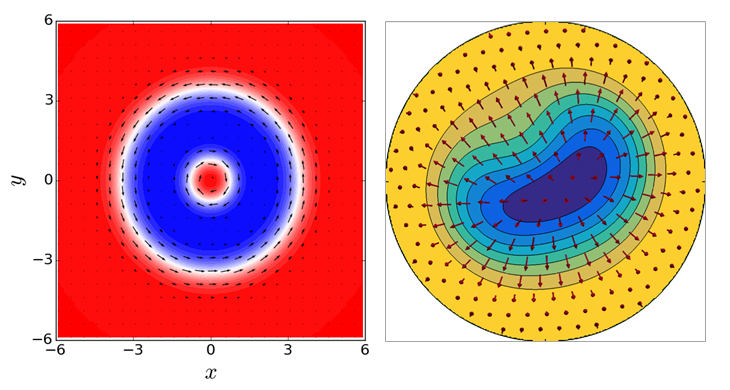
Semi-inverse methods: Closed form solutions that correspond to simple mechanical experiments are obtained from the system of momentum’s differential equations using semi-inverse methods. Simple tension/compression, indentation, wrinkling\buckling are examples of simple but important tests for the characterization of materials at the microscale. They serve as a guide for testing continuum theories of micro, nano materials against available experimental or computational results.

Optical beams and Structured light fields: Research in this area aims to the theoretical understanding and numerical simulation of optical waves in space and space-time, and their applications in different branches of optical engineering and photonics. The core of this activity concerns the generation of optical waves with engineered properties such as beam width, trajectory, and maximum amplitude, as well as the propagation of invariant optical fields of the Airy and Bessel-type, and their applications in high-resolution microscopy and stealth technologies .

Periodic lattices: Research in this area deals with specific nonlinear aspects of light propagating in complex systems with periodic optical indices. Especially we focus on the dynamics in different types of lattices and the understanding of topological phenomena, gauge fields, dynamic localization and coherent destruction of tunneling, and also the interplay between pseudospin, isospin, and vorticity in photonic graphene.

Nonlinear dynamics in magnetic materials: Research in this area aims to the investigation of the rich micromagnetic structure and the description of a variety of patterns at the mesoscale and the nanoscale. Physico-mathematical studies in this field focus on magnetic solitons, which are topological in nature, and they are motivated by and combined with the strong technological interest from the high-tech industry on magnetic materials, including magnetic storage, magnetoresistive-RAM applications, spin-torque oscillators, and magnetic diodes. The models include domain walls in one spatial dimension, vortices and skyrmions in two dimensions, and vortex rings in three dimensions, and they are modeled by various forms and generalisations of the Landau-Lifshitz equation, which lead to different interesting and useful dynamics of topological magnetic solitons.

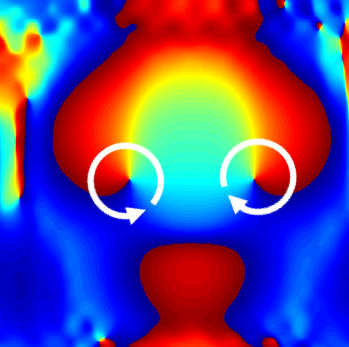
Solitons in condensed matter physics: Topological solitons arise in a great variety of condensed matter systems, as well as in cosmology and in nonlinear optics. The research in this direction focus on the investigation of ultra-cold gases that form Bose-Einstein condensates (BECs), which are of particular interest to quantum technology. Quantised vortices (or superfluid vortices) are found as solutions of Gross-Pitaevskii models. The tunability of gaseous BECs allows for complicated structures, such as vortex rings that propagate in a cylindrical BEC, to be formed. The study of these systems is based on the theory of conservation laws and the numerical simulation of the nonlinear model.

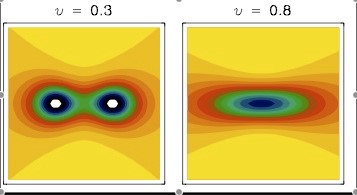
Semiclassical modeling of wave and quantum systems: Research in this direction focuses on the semiclassical asymptotics of wave and Schrodinger equations, via phase space techniques, which are very powerful for the construction of uniform (caustic-free) solutions of the Cauchy problem with highly oscillatory data, and the investigation of propagating singularities and beam-type solutions, in acoustics, seismology, optics and quantum mechanics. Techniques from microlocal analysis (Fourier integral operators) and deformation quantization (Wigner and wave-packet transforms) are employed to device phase space equations governing energy density and flux propagation. Asymptotic solutions are constructed using stationary phase approximations for complex phases, that are able to describe essential wave and quantum effects in phase space far away from classical Lagrangian manifolds.

Education and Training: The group contributes to the education and training of undergraduate, graduate and post-graduate students as well as of PhD candidates and Postdoctoral researchers.

Mesoscale & Continuum Modelling

RESEARCH AND DEVELOPMENT PROGRAMS

A. ONGOING PROJECTS

Title: SINGinGR: Singularities in General Relativity
Founding Agency: ERCEA (European Research Council Executive Agency)
Duration: 1/3/2024 - 31/3/2028
Title: “Using pin beams and complex beam profiles to optimize the performance of free space optical links”
Funding agency and funding scheme: Research cooperation between HUAWEI TECHNOLOGIES SWEDEN AB and FORTH
Duration: 2022-2024

B. COMPLETED PROJECTS

Title: ThunderSKY: Theoretical Understanding of static and dynamic properties of Skyrmions: towards a skyrmion-based technology,
Funding Agency and funding scheme: Hellenic Foundation for Research and Innovation (H.F.R.I.), «1st Call for H.F.R.I. research projects to support Postdoctoral Researchers»
Duration: 2018-2022.

PUBLICATIONS

2024
- NK Efremidis, DN Christodoulides (2024) Statistical mechanics and pressure of composite multimoded weakly nonlinear optical systems, arXiv preprint arXiv:2404.02745
- G Fournodavlos, E Marshall, TA Oliynyk (2024) Future stability of perfect fluids with extreme tilt and linear equation of state p=c^2_sρ for the Einstein-Euler system with positive cosmological constant: The range 1/3 < c^2_s < 3/7, arXiv preprint arXiv:2404.067897
- TJ Healey, R Paroni, P Rosakis (2024) Sharp-interface limits for brittle fracture via the inverse-deformation formulation, arXiv preprint arXiv:2403.00838
- H Ren, GG Pyrialakos, FO Wu, NK Efremidis, M Khajavikhan, DN Christodoulides (2024) Dalton’s law of partial optical thermodynamic pressures in highly multimoded nonlinear photonic systems, Optics Letters 49 (7), 1802-1805.
- D Sfyris (2024) Classical elastodynamics as a linear symmetric hyperbolic system in terms of (u_x, u_t), Journal of Elasticity 156 (2024) 525-548 doi: 10.1007/s10659-024-10059-8.
- D Sfyris, R. Bustamante, K.R. Rajagopal (2024) On the hyperbolicity of the governing equations for the linearization of a class of implicit constitutive relations. Mechanics Research Communications, 138 (2024) 104291. https://doi.org/10.1016/j.mechrescom.2024.104291
- D Sfyris, GI Sfyris (2024) Elastodynamics of multilattices: field equations of the linear theory as a first order system. Journal of Elasticity, https://doi.org/10.1007/s10659-024-10076-7
- D Sfyris, GI Sfyris (2024) Linear elastic diatomic multilattices: Three-dimensional constitutive modeling and solutions of the shift vector equation, Mathematics and Mechanics of Solids, 29 (2024) 1413-1431. https://doi.org/10.1177/10812865231217464
2023
- D Bachmann, M Lianeris, S Komineas (2023) Meron configurations in easy-plane chiral magnets, Physical Review B 108 (1), 014402.
- Chatziafratis, A., Kamvissis, S., Stratis, I.G. Boundary behavior of the solution to the linear Korteweg-De Vries equation on the half line, Studies in Applied Mathematics (2023) 150 (2), pp. 339-379.
- X Chen, P Rosakis, Z Wu, Z Zhang (2023) Solving nonconvex energy minimization problems in martensitic phase transitions with a mesh-free deep learning approach, Computer Methods in Applied Mechanics and Engineering 416, 116384.
- S Droulias, M Loulakis, DG Papazoglou, S Tzortzakis, Z Chen, N Efremidis (2023) Inverted pin beams for robust long-range propagation through atmospheric turbulence, Optics Letters 48 (21), 5467-5470.
- S Komineas (2023) Non-Hermitian dynamics for a two-spin system with PT symmetry, Physical Review B 107 (9), 094435.
- Komineas, S., Melcher, C., Venakides, S. Chiral magnetic skyrmions across length scales, New Jounal of Physics (2023) 25 (2), art. no. 023013.
- Pervolarakis, E., Tritsaris, G.A., Rosakis, P., Remediakis, I.N. Machine Learning for the edge energies of high symmetry Au nanoparticles, Surface Science (2023) art. no. 122265.
- H Ren, GG Pyrialakos, FO Wu, PS Jung, N Efremidis, M Khajavikhan, D Christodoulides (2023) Nature of Optical Thermodynamic Pressure Exerted in Highly Multimoded Nonlinear Systems, Physical Review Letters 131 (19), 193802.
- Sfyris, D., Sfyris, G.I., Linear theory of 2 and 3-monoatomic multilattices: solutions of the shift vector equation, Cont. Mech. Thermod. (2023) 35, 1927-1942.
- Sfyris, D., Sfyris, G.I., Breakdown of smooth solutions in one dimensional nonlinear nonlocal elasticity, Mech,. Res. Commun. (2023) 129, 104092.
- Sfyris, D., Sfyris, G.I. Constitutive modeling of three-dimensional monoatomic linear elastic multilattices, Math. Mech. Sol. (2023) 28, 973-988.
- G Theodorou, S Komineas (2023) Interaction and collision of skyrmions in chiral antiferromagnets, arXiv preprint arXiv:2305.13515
2022
- Karageorge, P.D., Makrakis, G.N. Asymptotic approximations for the phase space Schrödinger equation, Journal of Physics A: Mathematical and Theoretical (2022) 55 (34), art. no. 345201.
- Efremidis, N.K., Christodoulides, D.N. Thermodynamic optical pressures in tight-binding nonlinear multimode photonic systems, Communications Physics (2022) 5 (1), art. no. 286.
- Komineas, S., Roy, P.E. Breathing skyrmions in chiral antiferromagnets, Physical Review Research (2022) 4 (3), art. no. 033132.
- Grekas, G., Koumatos, K., Makridakis, C., Rosakis, P. Approximations of energy minimization in cell-induced phase transitions of fibrous meterials: Γ-convergence analysis, SIAM Journal of Numerical Analysis (2022) 60 (2), pp. 715-750.
- Sfyris, D., Sfyris, G.I. Conditions for hyperbolicity and approximate Riemann invariants in one dimensional nonlinear nonlocal elasticity Mechanics Reserach Communications (2022) 126, art. no. 104017.
2021
- Rosakis, P., Healey, T.J., Alyanak, U. The inverse-deformation approach to fracture, Journal of the Mechanics and Physics of Solids (2021) 150, art. no. 104352, .
- Grekas, G., Proestaki, M., Rosakis, P., Notbohm, J., Makridakis, C., Ravichandran, G. Cells exploit a phase transition to mechanically remodel the fibrous extracellular matrix, Journal of the Royal Society Interface (2021) 18 (175), art. no. 20200823.
- Hatzizisis, N., Kamvissis, S. Semiclassical WKB problem for the non-self-adjoint Dirac operator with a decaying potential, Journal of Mathematical Physics (2021) 62 (3), art. no. 033510.
- Efremidis, N.K. Topological photonic Su-Schrieffer-Heeger-type coupler, Physical Review A (2021) 104 (5), art. no. 053531.
- Bongiovanni, D., Denghui, L.I., Goutsoulas, M., Hao, W.U., Yi, H.U., Song, D., Morandotti, R., Efremidis, N.K., Chen, Z. Free-space realization of tunable pin-like optical vortex beams, Photonics Research (2021) 9 (7), pp. 1204-1212.
- Efremidis, N.K., Christodoulides, D.N. Fundamental entropic processes in the theory of optical thermodynamics, Physical Review A (2021) 103 (4), art. no. 043517.
- Ren, H., Wu, F.O., Jung, P., Efremidis, N.K., Khajavikhan, M., Christodoulides, D.N. Establishing a rigorous relation between thermodynamic and electrodynamic pressures in highly multimoded nonlinear dielectric waveguides, Optics InfoBase Conference Papers (2021) art. no. FW2L.7.
- Goutsoulas, M., Efremidis, N.K. Dynamics of self-accelerating electron beams in a homogeneous magnetic field, Physical Review A (2021) 103 (1), art. no. 013519.
- Tomasello, R., Komineas, S. Vortex propagation and phase transitions in a chiral antiferromagnetic nanostripe, Physical Review B (2021) 104 (6), art. no. 064438.
- Komineas, S., Melcher, C., Venakides, S. Chiral skyrmions of large radius, Physica D: Nonlinear Phenomena (2021) 418, art. no. 132842.
- Sisodia, N., Muduli, P.K., Papanicolaou, N., Komineas, S. Chiral droplets and current-driven motion in ferromagnets, Physical Review B (2021) 103 (2), art. no. 024431.
- Sfyris, D., Dragatogiannis, D.A., Charitidis, C. Nonlinear elastic constitutive modeling of α-Ge, Int. J. Nonlinear Mechanics (2021) 134, art. no. 103737.
- Manolis, G.D., Dineva, P.S., Rangelov, T., Sfyris, D. Mechanical models and numerical simulations in nanomechanics: A review across the scales, Engng. Anal. with Boundary Elements (2021) 128, pp. 149-170.
2020
- Rosakis, P., Marketou, M.E. Rethinking case fatality ratios for covid-19 from a data-driven viewpoint, Journal of Infection (2020) 81 (2), pp. e162-e164.
- Zhang, Z., Rosakis, P., Hou, T.Y., Ravichandran, G. A minimal mechanosensing model predicts keratocyte evolution on flexible substrates, Journal of the Royal Society Interface (2020) 17 (166), art. no. 20200175.
- Fujiié, S., Kamvissis, S. Semiclassical WKB problem for the non-self-Adjoint Dirac operator with analytic potential, Journal of Mathematical Physics (2020) 61 (1), art. no. 011510.
- Komineas, S.and N. Papanicolaou, N., Traveling skyrmions in chiral antiferromagnets, SciPost Phys. (2020) 8, 086.
- Komineas, S., Melcher, C., Venakides, S. Chiral skyrmions of large radius (2020) arXiv:1910.04818.
- Komineas, S., Melcher, C., Venakides, S., The profile of chiral skyrmions of small radius Nonlinearity (2020) 33, 3395-3408.
- Bongiovanni, D., Li, D., Goutsoulas, M., Morandotti, R., Song, D., Efremidis, N.K., Hu, Y., Chen, Z. Generation of Vortex Optical Pin-like Beams, IEEE Photonics Conference, IPC 2020 – Proceedings (2020) art. no. 9252464.
- Li, D., Bongiovanni, D., Goutsoulas, M., Xia, S., Zhang, Z., Hu, Y., Song, D., Morandotti, R., Efremidis, N.K., Chen, Z. Direct comparison of anti-diffracting optical pin beams and abruptly autofocusing beams, OSA Continuum (2020) 3 (6), pp. 1525-1535.
- Li, D., Bongiovanni, D., Goutsoulas, M., Hu, Y., Song, D., Morandotti, R., Efremidis, N.K., Chen, Z. Pin-Like Optical Vortex Beams, Conference Proceedings - Lasers and Electro-Optics Society Annual Meeting-LEOS, 2020-May, art. no. 9192130.
- Goutsoulas, M., Bongiovanni, D., Li, D., Chen, Z., Efremidis, N.K. Tunable self-similar Bessel-like beams of arbitrary order, Optics Letters (2020) 45 (7), pp. 1830-1833.
- Li, D., Bongiovanni, D., Goutsoulas, M., Hu, Y., Song, D., Morandotti, R., Efremidis, N.K., Chen, Z. Pin-like optical vortex beams, Optics InfoBase Conference Papers (2020) Part F182-CLEO-QELS 2020.
- Bongiovanni, D., Li, D., Goutsoulas, M., Hu, Y., Song, D., Morandotti, R., Efremidis, N.K., Chen, Z. Demonstration of vortex optical pin beams, Optics InfoBase Conference Papers (2020) Part F187-NP 2020.
2019
- Komineas, S., C. Melcher, C., Venakides, S., Traveling domain walls in chiral ferromagnets Nonlinearity (2019) 32, 2392-2412.
- Sisodia, N., Komineas, S., Muduli, P.K., Chiral skyrmion auto-oscillations in a ferromagnet under spin transfer torque, Phys. Rev. B (2019) 99, 184441.
- Roussou, A., Smyrnakis, J., Magiropoulos, M., Efremidis, N.K., Von Klitzing, W., Kavoulakis, G.M. Fragility of the bosonic Laughlin state, Physical Review A (2019) 99 (5), art. no. 053613.
- Efremidis, N.K., Chen, Z., Segev, M., Christodoulides, D.N. Airy beams and accelerating waves: An overview of recent advances, Optica (2019) 6 (5), art. no. 354553, pp. 686-701.
- Zhang, Z., Liang, X., Goutsoulas, M., Efremidis, N., Chen, Z. Demonstration of turbulence-resistant propagation of anti-diffracting optical beams beyond kilometer distances, Conference on Lasers and Electro-Optics, CLEO 2019 - Proceedings, art. no. 8749546.
- Song, D., Leykam, D., Su, J., Liu, X., Tang, L., Liu, S., Zhao, J., Efremidis, N.K., Xu, J., Chen, Z. Valley Vortex States and Degeneracy Lifting via Photonic Higher-Band Excitation, Physical Review Letters (2019) 122 (12), art. no. 123903.
- Zhang, Z., Liang, X., Goutsoulas, M., Efremidis, N., Chen, Z. Demonstration of turbulence-resistant propagation of anti-diffracting optical beams beyond kilometer distances, Optics InfoBase Conference Papers, Part F128-CLEO_QELS 2019.
2018
- Tomasello, R., Komineas, S., Siracusano, G., Carpentieri, M., Finocchio, G., Chiral skyrmions in an anisotropy gradient driven by spin-Hall effect, Phys. Rev. B 98, 024421 (2018).
2017
- Efremidis, N. K., Spatiotemporal diffraction-free pulsed beams in free-space of the Airy and Bessel type, Opt. Lett. (2017) 42, 5038.
- Goutsoulas, M., Paltoglou, V., Efremidis, N. K., Cross-phase modulation mediated pulse control with Airy pulses in optical fibers, J. Opt. (2017) 19, 115505.
- Efremidis, N. K., Nye, N. S., Christodoulides, D. N., Exact bidirectional X-wave solutions in fiber Bragg gratings, Phys. Rev. A (2017) 96, 043820.
- Roussou, A., Smyrnakis, J., Magiropoulos, M., Efremidis, N. K., Kavoulakis, G. M. Rotating Bose-Einstein condensates with a finite number of atoms confined in a ring potential: Spontaneous symmetry breaking, beyond the mean-field approximation, Phys. Rev. A (2017) 95, 033606.
- Paltoglou V., Efremidis, N. K., Breaking in a nonlinear double-slit configuration, J. Opt. Soc. Am. B (2017) 34, 257.
- Efremidis, N. K., Mparkas, M. Nonlinear imaging in photonic lattices, Opt. Lett. (2017) 42, 147.
2016
- Komineas, S., Shipman, S.P., Venakides, S., Lossless polariton solitons, Physica D (2016) 316, 43-56.
- Penciu, R.-S., Makris, K. G, Efremidis, N. K., Nonparaxial abruptly autofocusing beams, Opt. Lett. (2016) 41, 1042.
2015
- Notbohm, J., Lesman, A., Rosakis, P., Tirrell, D.A., Ravichandran, G., Microbuckling of fibrin enables long range cell mechanosensing, Journal of the Royal Society Interface (2015) 12 (108) 20150320. arXiv:1407.3510
- Komineas, S., Papanicolaou, N., Skyrmion dynamics in chiral ferromagnets under spin-transfer torque, Phys. Rev. B (2015) 92, 174405.
- Rosakis, P., Notbohm, J., Ravichandran, G., A Model for Compression-Weakening Materials and the Elastic Fields due to Contractile Cells, Journal of the Mechanics and Physics of Solids (2015) 85 16-32. arXiv:1412.2612.
- Roussou, A., Tsibidis, G. D., Smyrnakis, J., Magiropoulos, M., Efremidis, N. K., Jackson, A. D., Kavoulakis G. M. (2015) Hysteresis and metastability of Bose-Einstein condensed clouds of atoms confined in ring potentials, Phys. Rev. A (2015) 91, 023613.
- Song, D., Paltoglou, V., Liu, S., Zhu, Yi, Gallardo, D., Tang, L., Xu, J. Ablowitz, M., Efremidis, N. K, Chen Z., Unveiling pseudospin and angular momentum in photonic graphene, Nat. Commun. (2015) 6, 6272.
- Paltoglou, V., Chen, Z., Efremidis, N. K., Composite multi-vortex diffraction-free beams and van Hove singularities in honeycomb lattices, Opt. Lett. (2015) 40, 1037
- Wu, Z., Zaremba, E., Smyrnakis, J., Magiropoulos, M., Efremidis, N. K., Kavoulakis G.M., Mean-field yrast spectrum and persistent currents in a two-component Bose gas with interaction asymmetry, Phys. Rev. A (2015) 92, 033630.
- Zhao, J., Chremmos, I. D., Song, D., Zhang, P., Christodoulides, D. N., Efremidis, N. K., Chen, Z., Curved singular beams for three-dimensional particle manipulation, Sci. Rep. (2015) 5, 12086.
- Song, D., Liu, S., Paltoglou, V., Gallardo, D., Tang, L., Zhao, J., Xu, J., Efremidis, N. K., Chen Z., Controlled generation ofpseudospin-mediated vortices in photonic graphene, 2D Mater. (2015) 40, 034007.
- Zhao, J.; Chremmos, I. D.; Zhang, Ze; Hu, Yi; Song, D.; Zhang, P.; Efremidis, N. K. and Chen, Z., Specially shaped Bessel-like self-accelerating beams along predesigned trajectories, Sci. Bull. (2015) 60, 1157.
- Penciu, R.-S., Paltoglou, V., Efremidis N. K., Closed-form expressions for nonparaxial accelerating beams with pre-engineered trajectories, Opt. Lett. (2015) 40, 1444.
- Paltoglou V., Efremidis, N. K., Modifying the optical path in a nonlinear double-slit experiment, Opt. Lett. (2015) 40, 5208.
- Chen, Z., Zhao, J., Chremmos, I. D., Song, D., Christodoulides, D. N., Efremidis, N. K., Spiraling particles by fineshaped dynamical singular beams, Opt. Photonics News (2015) 26, 44.
- Rosakis, P., Continuum surface energy from a lattice model, Networks and Heterogeneous Media (2015) 9(3), 453-476.
- Komineas, S. and Papanicolaou, N., Skyrmion dynamics in chiral ferromagnets, Phys. Rev. B (2015) 92, 064412.
- Zhang, S., Baker, A.A., Komineas, S., Hesjedal, Th., Topological computation based on direct magnetic logic communication, Scientific Reports (2015) 5, 15773.
- Komineas, S., Shipman, S.P., Venakides, S., Continuous and discontinuous dark solitons in polariton condensates, Phys. Rev. B (2015) 91, 134503.
- Komineas, S., Magnetization oscillations by vortex-antivortex dipoles, Physica D (2015) 291, 8-16.
2014
- Efremidis N.K., Accelerating beam propagation in refractive index potentials, Phys. Rev. A (2014) 89, 023841.
- Makris, K. G., Kaminer, I., El-Ganainy, R., Efremidis, N. K., Chen, Z., Segev, M., Christodoulides, D. N., Accelerating diffraction-free beams in photonic lattices, Opt. Lett. (2014) 39, 2129
- Bolpasi, V., Efremidis, N. K., Morrissey, M. J., Condylis, P., Sahagun, D., Baker M., von Klitzing W. An ultra-brightatom laser, New J. Phys. (2014) 16, 033036.
- Smyrnakis, J., Magiropoulos, M., Efremidis, N. K., Kavoulakis, G.M., Persistent currents in a two-component Bose-Einstein condensate confined in a ring potential, J. Opt. B Quantum Semiclassical Opt. (2014) 47, 215302.
2013
- Zhao, J., Zhang, P., Deng, D., Liu, J., Gao, Y., Chremmos, I. D., Efremidis, N. K., Christodoulides, D. N., Chen, Z., Observation of self-accelerating Bessel-like optical beams along arbitrary trajectories, Opt. Lett. (2013) 38, 498.
- Efremidis, N. K., Paltoglou, V., von Klitzing, W., Accelerating and abruptly autofocusing matter waves, Phys. Rev. A (2013) 87, 043637.
- Chremmos, I. D., Fikioris, G., Efremidis, N. K., Accelerating and abruptly-focusing beam waves in the Fresnel zone of antenna arrays, IEEE Trans. Antennas Propag. (2013) 61, 5048.
- Chremmos, I. D., Efremidis, N. K., Nonparaxial accelerating Bessel-like beams, Phys. Rev. A (2013) 88, 063816.
- Finocchio, G., Puliafito, V., Komineas, S., Torres, L., Ozatay, O., Hauet, T., Azzerboni, B., Nanoscale spintronic oscillators based on the excitation of confined soliton modes, J. Appl. Phys. (2013) 114, 163908.

PEOPLE

RESEARCHERS

CONTACT US

For any information regarding the group please contact:

Mesoscale Modelling Group,
Institute of Applied and Computational Mathematics,
Foundation for Research and Technology - Hellas
Nikolaou Plastira 100, Vassilika Vouton,
GR 700 13 Heraklion, Crete
GREECE

Tel: +30 2810 391800
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it. (Mrs. Maria Papadaki)

Tel.: +30 2810 391805
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it. (Mrs. Yiota Rigopoulou)