ABOUT    R&D ACTIVITIES    R&D PROGRAMS    PUBLICATIONS    PEOPLE    CONTACT US

The Computational Biomechanics group develops novel, efficient, and accurate computational methods to address complex problems of practical interest, mainly in Bio Inspired Solid and Fluid Mechanics. Our efforts focus on advanced applications, an area where commercial software cannot compete with advanced numerical techniques. In the area of modelling mechanosensing and cell-ECM interactions with phase transitions and instability, the objectives are twofold:

(i) To develop and test nonlinear mathematical models of cell evolution / locomotion based on active mechanosensing, and to explain cell migration phenomena accordingly through simulation.

(ii) To investigate the nonlinearities in the mechanical behaviour of the fibrous extracellular matrix, to understand the instabilities that govern its behaviour, and to clarify how they result in a phase transition that is exploited by cells for mechanosensing and ECM remodelling. The tool here is modelling: we develop and test models of the ECM as a discrete fiber network and as a highly nonlinear continuum and investigate the similarities and differences of the two models using numerical analysis techniques to develop appropriate numerical methods.

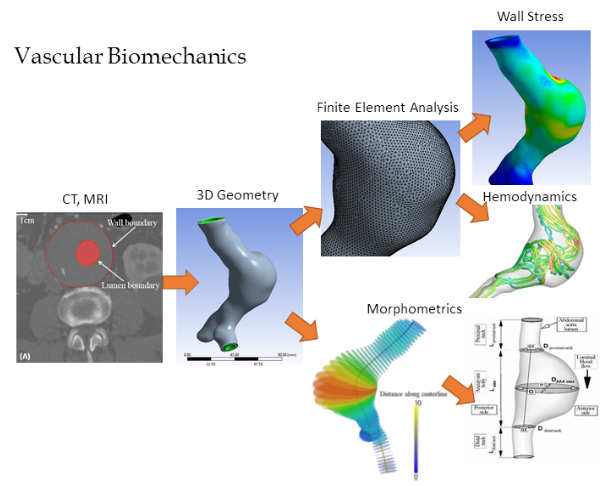
Biomedical Flows: We are investigating biomedical flows in both physiological and diseased segments of the vascular tree including complex geometrical configurations such as bifurcations, and are also working on accurate, cost-effective techniques for fluid-structure interaction. During this process we are developing new techniques for vascular surface reconstruction from data acquired through 3D medical imaging techniques. Surface reconstruction is currently needed for modelling purposes. The work on surface reconstruction can, however, be extended and automated so that fast three-dimensional reconstruction of vital organs, such as liver and kidneys, becomes possible. This capability is of interest to medical practitioners, at least at a national level, because it can directly provide them with three-dimensional images instead of two-dimensional cross sections. We have also developed a novel non rigid registration based method for the computation of arterial surface growth distribution applied to assess Abdominal Aortic Aneurysm evolution. Local surface growth rate could be a useful index in estimating risk of rupture.

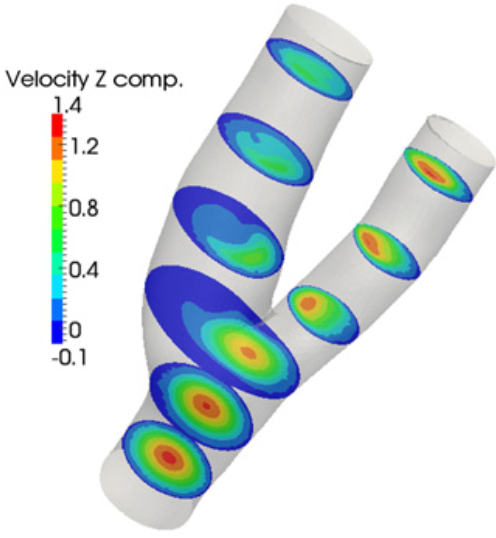
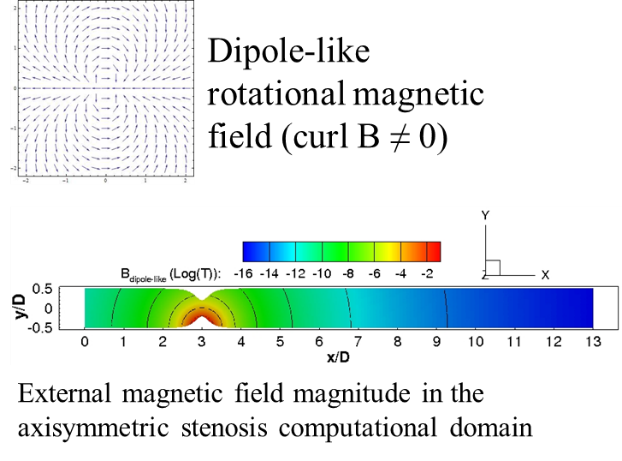
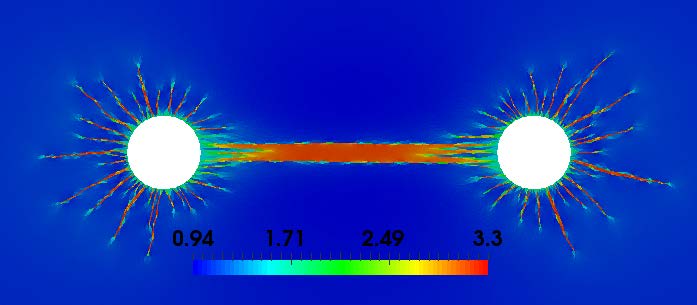
Magneto-Hemodynamics: In the science of magnetohydrodynamics, most of the attention is devoted to fluids that are electrical conductors, that is, fluids that feature the presence of electrical charges (positive, negative ions and free electrons). On the other hand, studies that address theoretically, numerically and experimentally the properties of polarizable and magnetizable fluids (PMFs) are scarce. Molecules of PMFs are characterized by non-vanishing electric- and magnetic-dipole moments and, therefore, their motion can be influenced by (gradients of) electromagnetic fields; the presence of (free) electric charges is not needed. 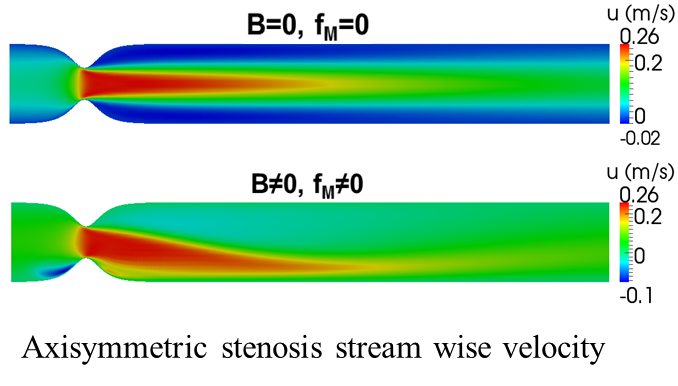Magnetohaemodynamics may have an impact in medicine, control of steady and pulsatile flow through vascular and heart valve stenosis, or control of turbulence for prevention of haemodialysis graft failure. We investigate the effects of the magnetic field in the flow that develops: in both idealized and realistic, image-based, arterial bifurcation models with our without stenosis. Arterial bifurcations are sites of significant pathophysiological interest in the vascular system due the complex 3D flow field that develops in their vicinity. The disturbed flow conditions that are associated with arterial bifurcations have been implicated in the initiation and progression of arterial wall disease leading to atheromatic stenosis of the vascular lumen and in the case of the carotid bifurcation to an increased risk of stroke. The post-stenotic flow regime which is characterized by significant flow instabilities that create structural vibrations is also of pathophysiological importance as it is believed to contribute to the development of post-stenotic dilatation of the arterial wall. Both steady state and transient flow are investigated with blood modeled as either a Newtonian or a non-Newtonian, incompressible fluid.

Modelling and Simulation of Mechanosensing in Cellular Locomotion:  We are investigating cellular shape evolution of locomoting cells on deformable substrates by combining ideas of mechanosensing with advanced computational techniques for studying shape evolution,  using the level set method. We have developed new models for the evolution of locomoting fish epidermal keratocytes using a novel local active  mechanosensing hypothesis: cells contract their substrate and the lamellipodium evolves locally according to a local mechanosensing law, according to the local stress field caused by cellular contraction. Our model is tuned by iterative comparison of simulation with observed behaviour and captures a multitude of characteristic types of response. Our work sheds new light on the role of mechanosensing in cell migration and locomotion.

 

Computation of Instabilities and Phase transitions in Biomaterials: Our work in continuum modelling has revealed that fibrous biomaterials undergo a densification phase transition because of a microbuckling instability of individual fibers in compression.  This means that deformations can have gradient discontinuities that cannot be accurately captured by ordinary numerical techniques.  We have developed novel finite element approaches to handle problems with discontinuous strains that we encountered  in fibrous biomaterials. Coupled with modelling, our simulations provide an unusual degree of success in predicting experimental observations, including geometrically complex intercellular patterns that arise when cellular contraction triggers the phase transition.

Education and Training: The group contributes to the education and training of undergraduate, graduate and post-graduate students as well as of PhD candidates and Postdoctoral researchers.

A. ONGOING PROJECTS

• LAMIA: Functional Nanoclusters for Multimodal Imaging of Atherosclerosis,
  Funding Source: FORTH-SYNERGY grant
  Duration: 2021-2024.

B. COMPLETED PROJECTS

• VITAD: Studying mechanisms of cellular response to shear stress and 3D substrate topography (In collaboration with the Institute of Electronic Structures and Laser). Advanced research activities in biomedical technology.
  Funding Source: Joint Research and Technology Programmes, General Secretariat for Research and Technology (GSRT), Greece
  Duration: 2017-2020.
• Hemodynamic factors associated with the initiation of aortic aneurysm disease,
  Funding Source: EPFL FORTH collaborative grant
  Duration: 2016 -2017.
  
• BIOSYS: Bio inspired computational simulations at cellular and organ scales. Development of interdisciplinary research activities in systems biology.
  Funding Source: Joint Research and Technology Programmes, General Secretariat for Research and Technology (GSRT), Greece
  Duration: 2014-2016.
• Simulations of High Enthalpy Compressible Turbulent Flows.
  Funding Source: France-Greece, Joint Research and Technology Programmes, General Secretariat for Research and Technology (GSRT), Greece
  Duration: 2013-2015.
  
• AAA Risk Assessment-Integrating morphologic, biomechanic, molecular and clinical risk factors to improve decision making in the management of abdominal aortic aneurysm disease,
  Funding Source: General Secretariat for Research and Technology (GSRT), Greece
  Duration: 2012 -2015.

RESEARCHERS

• Yannis Papaharilaou, Research Director
• Phoebus Rosakis, Professor, University of Crete
• Lika, Konstadia,  Professor, University of Crete
• Daphne Manoussaki, Assist. Professor, University of Crete
  
• Carmen Belloso Marrec, MCSA ESR Fellow

For any information regarding the group please contact:

Computational Biomechanics group,
Institute of Applied and Computational Mathematics,
Foundation for Research and Technology - Hellas
Nikolaou Plastira 100, Vassilika Vouton,
GR 700 13 Heraklion, Crete
GREECE

Tel: +30 2810 391800
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it. (Mrs. Maria Papadaki)

Tel.: +30 2810 391805
E-mail: This email address is being protected from spambots. You need JavaScript enabled to view it. (Mrs. Yiota Rigopoulou)