Deep learning: Deep learning has recently been at the forefront of artificial intelligence (AI) research and has truly revolutionized several fields of AI. Data Science Group members are actively involved in developing methods that can help us both better understand the limitations of existing deep learning approaches and also improve various aspects of their performance. They have worked on a wide variety of topics from this area, exploring both fundamental questions and practical applications. This includes, to mention a few of these topics, exploring and proposing novel deep network architectures, developing new ways of effectively transferring knowledge between networks, revisiting weight parameterizations for deep networks in order to improve their generalization capabilities, proposing novel self-supervised and few-shot learning methods, devising and applying learning approaches that advance the state-of-the-art for fundamental problems from the areas of computer vision and image analysis, making use of attention in the context of knowledge distillation, proposing hybrid (scattering-based) convolutional network architectures that allow for better representation learning and more interpretable features, as well as properly adapting deep neural networks such that they can be applied to arbitrary graph-structured data directly and can also handle structured-prediction tasks.

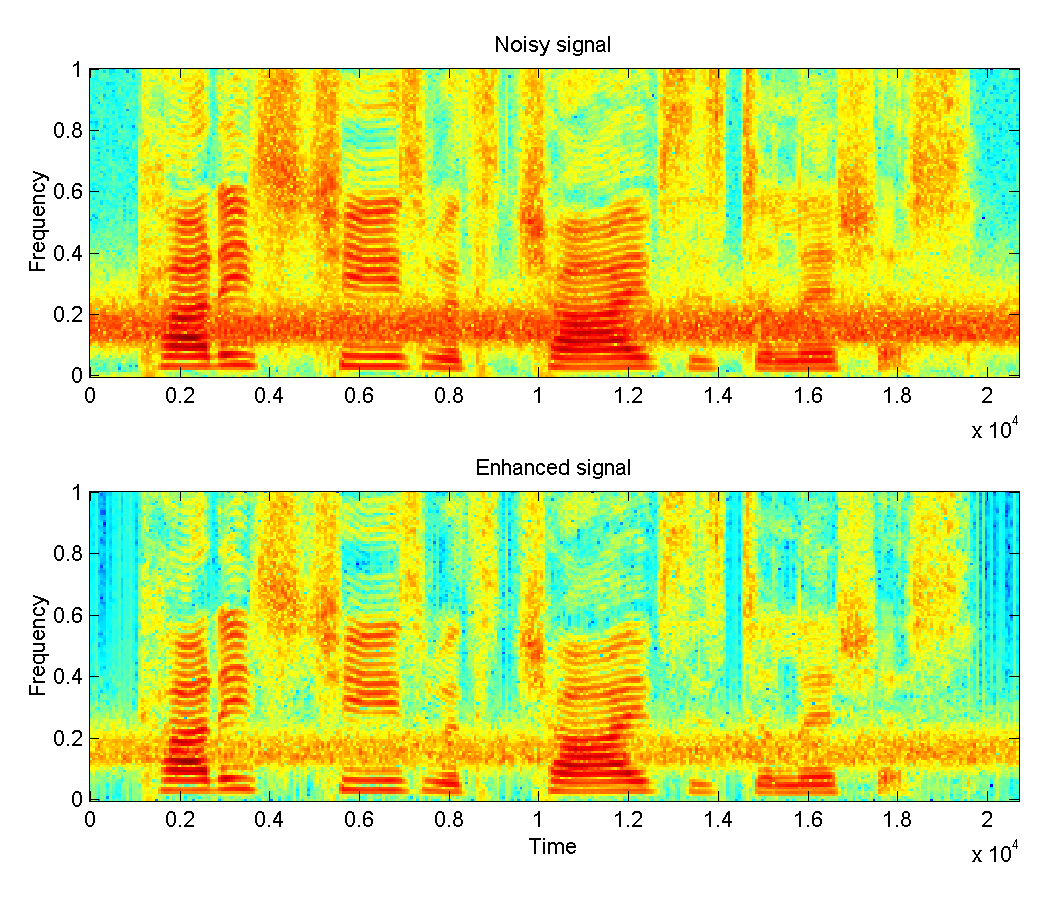
Neural-based Speech Synthesis - Deep Learning in Speech Processing: Deep Neural Networks have taken the engineering community by storm. Data-rich areas such as image processing and speech processing have been transformed during the last years. The Data Science Group combines its expertise on speech processing and applies deep learning techniques to applications such as voice conversion, speech synthesis and speech enhancement.

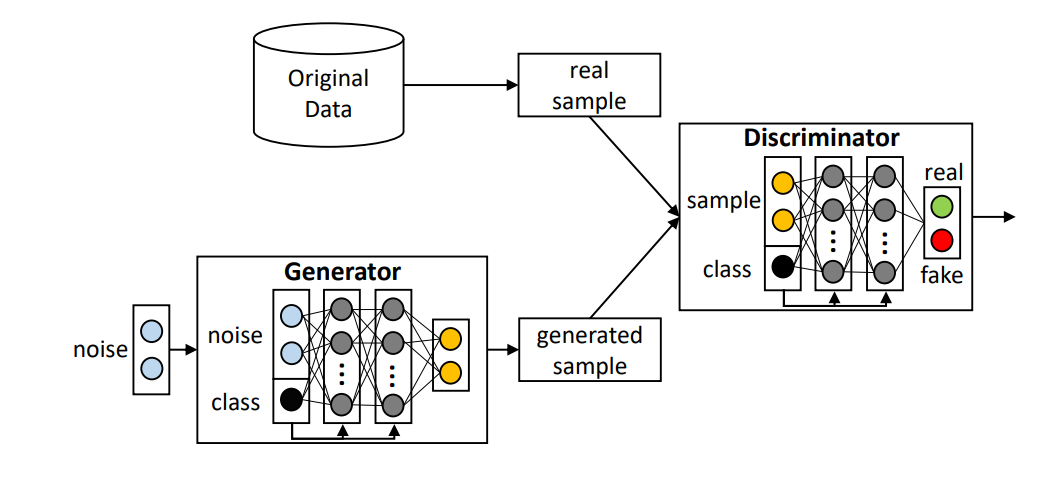
Generative Adversarial Nets - Deep Generative Learning:  Generative models based on Deep Neural Nets have shown unprecedented capabilities in sampling data from complex but unknown distributions. Researchers in the Data Science Group develop novel algorithms for training generative models, focusing on Generative Adversarial Networks (GANs). GANs have been used in data augmentation schemes to generate synthetic data that follow the same distributional characteristics as the original dataset (which may contain sensitive information or limited number of cases). The proposed methodology has been applied to identify dyslexia in children, using measurements from specialized eye trackers.

Space-time models: Data Science Group members are actively involved in the development of Bayesian and frequentist models for spatio-temporal data, including models with spatially varying coefficients. Conditional autoregressive priors, Moran’s eigenvector filtering, dimension reduction algorithms, penalized LASSO-type estimates and bootstrap-based uncertainty quantification are among the methodological tools that are used to estimate parameters and conduct inference on such models. Typical applications of space-time models in Geosciences include a) the evaluation of outputs from Regional Climate Models and b) the analysis of time series of remotely sensed imagery. Similar models have been developed to analyze the dynamics of regional economic variables.

Incident/Anomaly Detection: Group members develop real-time algorithms for incident/anomaly detection, focusing mostly on network activity (e.g. vehicular networks).  Decision trees and (nonparametric) quantile regressions are among the methodological tools that have been employed as key components of such algorithms. Typical applications include incident detection on vehicular networks based on loop detector data, fraud detection in bank transactions, etc.

Functional Data Analysis: Functional data analysis (FDA) focuses on data that can be curves, surfaces or anything else varying over a continuum. For instance, plasma thermograms are curves associated with a person’s health status; a group of such curves can be analyzed using FDA-analogues of conventional statistical procedures. The Data Science group develops segment-wise supervised classification schemes for multivariate functional data, which may reject noisy domains of the functional data and assign larger weights to segments that contain useful information for the classification groups of each study. A typical application of the proposed algorithms is disease identification/diagnosis.

Forecasting Multivariate Time Series: The group’s activities include research on linear (ARIMA) and nonlinear (smooth-transition or threshold autoregressions) parametric time series models that are estimated using a) fast penalized LASSO-type estimators or, b) Bayesian posteriors based on shrinkage priors (e.g. horseshoe). Such models are used in (real-time) forecasting applications, including for example, short-term forecasts of a) vehicular counts in a transportation network, b) energy outputs from wind- or solar-panel farms and c) emissions from heavy-duty diesel engines.

Statistical Analysis of Transportation Emissions: The group’s activity emphasizes predictive modeling of high-frequency emissions rates from real-world experiments, similar to the ones conducted to define European and US emissions standards. Such models typically focus on pollutants which are hard to measure, such as particle numbers (PN). The implemented methodology a) combines parametric nonlinear time series models with robust quantile regressions for vehicle-specific predictions, and b) estimates multi-level specifications to compute predictions for homogeneous families of vehicles.

Predictive Models in Biomedical Engineering and Epidemiology: The group’s activities include a) predictive modeling for heart volumes which are used to perform virtual heart transplants, b) spatial statistical specifications for the growth of thrombus in abdominal aortic aneurysms, c) nonparametric functional classifiers for disease identification and d) spatio-temporal models for epidemics.

Space-time Econometrics: Data Science group members constructed space-time models which aim to explain the dynamics of regional productivity in the EU. Currently, our group develops spatial and spatiotemporal models for the adoption of agricultural innovation in the US.

Sparse Inference in Dynamical Systems: The Data Science group members develop methods and algorithms for learning the structure and the parameters of sparse dynamical systems from temporal measurements. Sparsity means that the dynamics of each state variable are typically driven by a relatively small number of variables. Sparsity is critical for learning large systems from finite data and constitutes a form of complexity penalization and regularization thus favoring simpler solutions. Applications include but are not limited to biological networks of proteins, neuroscience, physics and finance.

Bayesian Networks: Bayesian networks, a special case of directed acyclic graphs, are frequently employed for modelling domain knowledge in Decision Support Systems, particularly in medicine. Researchers from the Data Science Group develop algorithms for Bayesian network structure learning, which can be used to automatically construct Decision Support Systems.

Feature Selection for Big and High-Dimensional Data: Feature (also called variable) selection for regression and classification, is an essential problem that has been given considerable attention during the last three decades. Specifically, feature selection is critical in order to construct models which possess a) satisfactory predictive capability and b) interpretable structure. The Data Science Group designs feature-selection algorithms that can be utilized in challenging applications that analyze Big data, in which the number of features may be larger than the number of cases (which can be in the order of millions).  The developed algorithms can be implemented in numerous and diverse research domains; a typical application is the analysis of SNP data (Bioinformatics).

Uncertainty Quantification in Stochastic Systems and Multilevel Models: Uncertainty quantification (UQ) is essential for the reliable and robust modelling of complex stochastic dynamics. The Data Science Group develops novel information-theoretic tools to address the challenges concerning the feasibility and efficiency of UQ in stochastic systems, which were used to analyze biological reaction networks. Furthermore, the Data Science group members conduct research on computationally intensive methods (e.g. bootstrap-based confidence intervals) for uncertainty quantification in models that capture nested data structures (multilevel models for categorical responses).

Parametric Sensitivity Analysis in Biochemical Reaction Networks: Data Science group members have developed parametric sensitivity analysis tools as an approach to mathematically and computationally understand and evaluate the behavior of complex phenomena in biochemical reaction networks.

Mathematics of information: Information is a core notion in many engineering and scientific disciplines. For example, much of modern statistics may be characterised as the process of extracting information from data. Over the past 60 years, information, along with its mathematical description via the Boltzmann-Shannon entropy, have played a crucial role in science and technology, both as a central metaphors providing intellectual guidelines, as well as a mathematically specific, technical, and precisely measurable quantities. Members of the Data Science group have been exploring the development of rigorous tools for the mathematical description of information, as well as the analysis of practical questions arising in a variety of applications, ranging from moder digital communications networks to finance, neuroscience and bioinformatics. 

Compositional Data Analysis: Compositional data are met in many different fields, such as economics, archaeometry, ecology, geology and political sciences. Researchers from the Data Science Group have worked on the improvement of existing predictive models (e.g. regression and classification) for compositional data, which can be seen as vectors of proportions that sum to one.

Heart Rate Estimation: Estimation of hazard rates is important in research areas such as reliability and survival analysis. The classical method of estimation involves modelling the failure times by appropriate probability distributions such as exponential, gamma, Weibull, etc. The Data Science Group focuses on nonparametric kernel methods, which are flexible as they are not based on distributional assumptions.

Supervised and Unsupervised Modeling: Researchers from the Data Science Group participate in projects that require the design, implementation, validation and deployment of a predictive model. Applications are diverse, including energy production forecasting for wind farms, outbreak forecasting, Raman spectroscopy, materials' properties prediction and more.

The group contributes to the education and training of undergraduate, graduate and post-graduate students as well as of PhD candidates and Postdoctoral researchers.

Further, the group contributes to the Postgraduate Program "Data Analysis & Machine-Statistical Learning" at the University of Crete. Members of the Data Science group participate in the above program as instructors and mentors. 

• G Baxevani, V Harmandaris, E Kalligiannaki, I Tsantili (2023) Bottom-up transient time models in coarse-graining molecular systems, arXiv preprint arXiv:2302.05159.
• M Berta, L Gavalakis, I Kontoyiannis (2023) A Third Information-Theoretic Approach to Finite de Finetti Theorems, arXiv preprint arXiv:2304.05360
  
• J Birrell, Y Pantazis, P Dupuis, MA Katsoulakis, L Rey-Bellet, Function-space regularized Rényi divergences, The Eleventh International Conference on Learning Representations 2023.
• MT Costa, I Kontoyiannis, S Godsill (2023) Generalised shot noise representations of stochastic systems driven by non-Gaussian Lévy processes, arXiv e-prints, arXiv: 2305.05931
• A Chatzimentor, A Doxa, S Katsanevakis, AD Mazaris (2023) Are Mediterranean marine threatened species at high risk by climate change? Global Change Biology 29 (7), 1809-1821
• G Chatzinikolaou, K Stratigi, A Siametis, E Goulielmaki, A Akalestou-Clocher, I Tsamardinos, P Topalis, C Austin, B Bouwman, N Crosetto, J Altmüller, G Garinis (2023) XPF interacts with TOP2B for R-loop processing and DNA looping on actively transcribed genes, Science Advances 9 (45), eadi2095
  
• Georgoulis, E.H., Loulakis, M., Tsiourvas, A. Discrete gradient flow approximations of high dimensional evolution partial differential equations via deep neural networks (2023) Communications in Nonlinear Science and Numerical Simulation, 117, art. no. 106893.
• S Gidaris, A Bursuc, O Simeoni, A Vobecky, N Komodakis, M Cord, P Pérez, MOCA: Self-supervised Representation Learning by Predicting Masked Online Codebook Assignment, arXiv preprint arXiv:2307.09361, 2023.
• I Karagiannaki, K Gourlia, V Lagani, Y Pantazis, I Tsamardinos (2023) Learning biologically-interpretable latent representations for gene expression data: pathway activity score learning algorithm, Machine Learning 112 (11), 4257-4287
• K Konsta, A Doxa, S Katsanevakis, AD Mazaris (2023) Projected intensification of subsurface marine heatwaves under climate change (pdf file)
• I Kontoyiannis (2023) Context-tree weighting and Bayesian Context Trees: Asymptotic and non-asymptotic justifications, IEEE Transactions on Information Theory
• I Kontoyiannis (2023) Time Series Analysis with Bayesian Context Trees: Classical Asymptotics and Finite-n Bounds, 2023 IEEE International Symposium on Information Theory (ISIT), 2470-2475
  
• A Koutsimpela, M Loulakis, (2023) On the optimally controlled stochastic shallow lake, International Journal of Control, 1
  
• K Lakiotaki, Z Papadovasilakis, V Lagani, S Fafalios, P Charonyktakis, M Tsagris, I Tsamardinos (2023) Automated machine learning for Genome Wide Association Studies, Bioinformatics 39 (9), btad545
  
• T Le, J Li, R Ness, S Triantafillou, S Shimizu, P Cui, K Kuang, J Pei,F. Wang, M. Prosperi, Preface: The 2023 ACM SIGKDD Workshop on Causal Discovery, Prediction and Decision, The KDD'23 Workshop on Causal Discovery, Prediction and Decision, 2023 (html file)
• A Litsas, F Fraggelakis, GD Tsibidis, E Stratakis, Y Pantazis (2023) Inferring the Parameters of Ultrafast Lasers from Images with Surface Patterns, 2023 International Symposium on Image and Signal Processing and Analysis (ISPA)
• EM Loizidou, P Barbounakis, S Glentis, A Dimopoulos, M Anezaki, P Rouskas, I Kontoyiannis, N Demiris, K Rouskas, AS Dimas (2023) Periodic veganism in healthy individuals improves blood lipids, reduces low-grade inflammation, but impairs bone health: the FastBio study, medRxiv, 2023.05. 17.23290094
• M Loulakis (2023) Correction: On the Symmetry of the Diffusion Coefficient in Asymmetric Simple Exclusion, Journal of Statistical Physics 190 (11), 177
  
• M Loulakis, CG Makridakis, A new approach to generalisation error of machine learning algorithms: Estimates and convergence, arXiv preprint arXiv:2306.13784, 2023
  
• S Martinot, N Komodakis, M Vakalopoulou, N Bus, C Robert, E Deutsch, N Paragios, Differentiable Gamma Index-Based Loss Functions: Accelerating Monte-Carlo Radiotherapy Dose Simulation, International Conference on Information Processing in Medical Imaging, 485-496, 2023 (html file)
• S Martinot, N Komodakis, M Vakalopoulou, N Bus, C Robert, E Deutsch, N Paragios, PO-1802 Deep Particles Embedding: accelerating Monte-Carlo dose simulations, Radiotherapy and Oncology 182, S1526-S1527, 2023
• Mazaris,AD, Dimitriadis, C, Papazekou, M, Schofield, G, Doxa, A, Chatzimentor, A, Turkozan, O, Katsanevakis S, Lioliou A, Abalo-Morla S, Aksissou M, Arcangeli A, Attard V, Atttiri H, Hili EI,Atzori F, Belda EJ, Nakhla LB, Berbash AA, Bjorndal KA, Broderick AC, Camiñas JA, Candan O, Cardona I, Cetkovic I, Dakik N, Andrea de Lucia G, Dimitrakopoulos PS,  Diryaq S, Favilli C,  Fortuna, CM, Fuller WJ,  Gallon S, Hamza A, Jribi I,  Ben Ismail M, Kamarianakis, Y, Kaska Y Korro K,  Koutsoubas D, Lauriano G, Lazar B, March D, Marco A, Minotou C, Monsinjon JR, Naguib NM, Palialexis A, Piroli V, Karaa Sami K, Sönmez B, Sourbès L, Sözbilen, D, Vandeperre, F, Vignes, P, Xanthakis, M,  Köpsel, V, Peck, MA, Priorities for Mediterranean marine turtle conservation and management in the face of climate change, Journal of Environmental Management, Volume 339, 2023, 117805
• K Mouloudakis, F Vouzinas, A Margaritakis, A Koutsimpela, G Mouloudakis, V Koutrouli, M Skotiniotis, GP Tsironis, M Loulakis, MW Mitchell, G Vasilakis, IK Kominis (2023), Inter-species spin-noise correlations in hot atomic vapors, Physical Review A 108 (5), 052822.
• A Neufeld, A Papapantoleon, Q Xiang (2023) Model-free bounds for multi-asset options using option-implied information and their exact computation, Management Science 69 (4), 2051-2068.
  
• Ntroumpogiannis, A., Giannoulis, M., Myrtakis, N., Christophides, V., Simon, E., Tsamardinos, I. (2023) A meta-level analysis of online anomaly detectors, The VLDB Journal, 1-42.
• I Papageorgiou, I Kontoyiannis (2023) The Bayesian Context Trees State Space Model for time series modelling and forecasting, arXiv preprint arXiv:2308.00913       
• I Papageorgiou, I Kontoyiannis (2023) Context-tree weighting for real-valued time series: Bayesian inference with hierarchical mixture models, 2023 IEEE International Symposium on Information Theory (ISIT), 2464-2469
• I Papageorgiou, I Kontoyiannis (2023) Truly Bayesian entropy estimation, 2023 IEEE Information Theory Workshop (ITW), 497-502.
• I Papageorgiou, I Kontoyiannis (2023) Posterior representations for Bayesian Context Trees: Sampling, estimation and convergence, Bayesian Analysis 1 (1), 1-29.
• A Papapantoleon, D Possamaï, A Saplaouras (2023)
  Stability of backward stochastic differential equations: the general Lipschitz case, Electronic Journal of Probability 28, 1-56.
• P Petsas, M Tzivanopoulou, A Doxa, SF Sailley, AD Mazaris (2023) Climate change on sea currents is not expected to alter contemporary migration routes of loggerhead sea turtles, Ecological Modelling 475, 110220
• OD Røe, OTD Nguyen, Y Fotopoulos, V Lagani, I Tsamardinos, Prediction of 6-year risk of bladder cancer using the HUNT Lung Cancer Risk Model in ever-smokers: A HUNT study, Journal of Clinical Oncology 41 (16_suppl), e16581-e16581, 2023.
• K Rounis, D Makrakis, C Papadaki, A Monastirioti, L Vamvakas, K Kalbakis, K Gourlia, I Xanthopoulos, I Tsamardinos, D Mavroudis, S Agelaki (2023)
  Correction: Prediction of outcome in patients with non-small cell lung cancer treated with second line PD-1/PDL-1 inhibitors based on clinical parameters: Results from a prospective, single institution study, Plos one 18 (11), e0294382
  
• Simantiraki, O., Pantazis, Y., Cooke (2023) The effect of masking noise on listeners’ spectral tilt preferences, Proc. INTERSPEECH 2023, 3058-3062.
• S Singla, N Murali, F Arabshahi, S Triantafyllou, K Batmanghelich (2023) Augmentation by Counterfactual Explanation-Fixing an Overconfident Classifier, Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pp. 4720-4730.
  
• A Theocharous, GG Gregoriou, P Sapountzis, I Kontoyiannis (2023) Temporally Causal Discovery Tests for Discrete Time Series and Neural Spike Trains, arXiv preprint arXiv:2305.14131       
  
• GV Thomaidis, K Papadimitriou, S Michos, E Chartampilas, I Tsamardinos, A characteristic cerebellar biosignature for bipolar disorder, identified with fully automatic machine learning, IBRO Neuroscience Reports 15, 77-89 2023.
• GV Thomaidis, K Papadimitriou, S Michos, E Chartampilas, I Tsamardinos, Corrigendum to “A characteristic cerebellar biosignature for bipolar disorder, identified with fully automatic machine learning”, IBRO Neuroscience Reports 15, 178, 2023.
• S Triantafillou, F Jabbari, GF Cooper, Learning Treatment Effects from Observational and Experimental Data, International Conference on Artificial Intelligence and Statistics, 7126-7146, 2023
• A Tsavdaridou, A Doxa, AD Mazaris (2023) Towards achieving a twenty-fold increase in the coverage of freshwater species distributions within protected areas in Europe, Biological Conservation 285, 110233
• K Tzirakis, Y Kamarianakis, N Kontopodis, CV Ioannou, Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance, Bioengineering 10 (7), 776, 2023
• Tzirakis K, Kamarianakis Y, Kontopodis N, Ioannou CV. Classification of Blood Rheological Models through an Idealized Symmetrical Bifurcation. Symmetry. 2023; 15(3):630
• K Tzirakis, Y Kamarianakis, N Kontopodis, CV Ioannou, The Effect of Blood Rheology and Inlet Boundary Conditions on Realistic Abdominal Aortic Aneurysms under Pulsatile Flow Conditions, Bioengineering 10 (2), 272, 2023,
• L Van Mieghem, A Papapantoleon, J Papazoglou-Hennig (2023) Machine learning for option pricing: an empirical investigation of network architectures, arXiv preprint arXiv:2307.07657
  

• P Barmpounakis, N Demiris, I Kontoyiannis, GN Pavlakis, V Sypsa (2022) Evaluating the effects of second-dose vaccine-delay policies in European countries: A simulation study based on data from Greece, Plos one 17 (4), e0263977
• D Bartl, M Kupper, T Lux, A Papapantoleon, S Eckstein (2020) (appendix) Marginal and dependence uncertainty: bounds, optimal transport, and sharpness, SIAM Journal on Control and Optimization 60, 410–434.
• C Bayer, CB Hammouda, A Papapantoleon, M Samet, R Tempone (2022) Optimal damping with hierarchical adaptive quadrature for efficient Fourier pricing of multi-asset options in Lévy models, arXiv preprint arXiv:2203.08196
  
• Birrell, J., Dupuis, P., Katsoulakis, M.A., Pantazis, Y., Rey-Bellet, L. (f,Γ)-Divergences: Interpolating between f-Divergences and Integral Probability Metrics (2022) Journal of Machine Learning Research, 23, .
• Birrell, J., Katsoulakis, M.A., Pantazis, Y. Optimizing Variational Representations of Divergences and Accelerating Their Statistical Estimation (2022) IEEE Transactions on Information Theory, 68 (7), pp. 4553-4572.
• Biza, K., Tsamardinos, I., Triantafillou, S. Out-of-Sample Tuning for Causal Discovery (2022) IEEE Transactions on Neural Networks and Learning Systems, pp. 1-11.
• Bowler, S., Papoutsoglou, G., Karanikas, A., Tsamardinos, I., Corley, M.J., Ndhlovu, L.C. A machine learning approach utilizing DNA methylation as an accurate classifier of COVID-19 disease severity (2022) Scientific Reports, 12 (1), art. no. 17480, .
• S Bowler, G Papoutsoglou, A Karanikas, I Tsamardinos, MJ Corley, L Ndhlovu, Machine Learning Analysis of DNA Methylation in COVID-19 Disease, Topics in Antiviral Medicine, 75-76, 2022
  
• Doxa A, Almpanidou V, Katsanevakis S, Queirós A, Kaschner K, Garilao C, Kesner‐Reyes K, Mazaris AD (2022) 4D marine conservation networks: Combining 3D prioritization of present and future biodiversity with climatic refugia, Global Change Biology 28 (15), 4577-4588
  
• Doxa, A., Kamarianakis, Y., Mazaris, A.D. Spatial heterogeneity and temporal stability characterize future climatic refugia in Mediterranean Europe (2022) Global Change Biology, 28 (7), pp. 2413-2424.
• M Fasoulakis, E Markakis, Y Pantazis, C Varsos, Forward looking best-response multiplicative weights update methods for bilinear zero-sum games, International Conference on Artificial Intelligence and Statistics, 11096-11117, 2022
  
• A Fayomi, Y Pantazis, M Tsagris, ATA Wood, Cauchy robust principal component analysis with applications to high-deimensional data sets, arXiv preprint arXiv:2211.03181, 2022.
• M Fasoulakis, E Markakis, Y Pantazis, C Varsos (2022) Forward looking best-response multiplicative weights update methods for bilinear zero-sum games, International Conference on Artificial Intelligence and Statistics, 11096-11117.
  
• L Gavalakis, I Kontoyiannis (2022) Information-theoretic de Finetti-style theorems, 2022 IEEE Information Theory Workshop (ITW), 71-76
• L Gavalakis, I Kontoyiannis (2022) Information in probability: Another information-theoretic proof of a finite de Finetti theorem, Mathematics Going Forward: Collected Mathematical Brushstrokes, 367-385
• L Gavalakis, I Kontoyiannis (2022) The Entropic Central Limit Theorem for Discrete Random Variables, 2022 IEEE International Symposium on Information Theory (ISIT), 708-713
• Giovos I, Katsada D, Spyridopoulou RNA, Poursanidis D, Doxa A, Katsanevakis S, Periklis Kleitou P, Vasiliki Oikonomou V, Vasileios Minasidis V, Ayaka A Ozturk AA, Dimitra Petza D, Maria Sini M, Cahide Cigdem Yigin CC, Meyers E, Barker J, Jiménez-Alvarado D, Hood AR (2022) Strengthening angel shark conservation in the northeastern Mediterranean Sea, Journal of Marine Science and Engineering 10 (2), 269
• H Gu, P Birmpa, Y Pantazis, L Rey-Bellet, MA Katsoulakis, Lipschitz regularized gradient flows and latent generative particles, arXiv preprint arXiv:2210.17230, 2022.
• A Jamal, A Tzavaras Y Kamarianakis, Y Pantazis, E Kalligiannaki, T Katsaounis, K Kotsovos, I Gereige, M Abdullah, Efficiency evaluation and comparisons of solar cell technologies based on measurements from the Arabian peninsula, EuroSun, 1755-1766, 2022 (html file)
• A Jamal, A Tzavaras, Y Kamarianakis, Y Pantazis, E Kalligiannaki, TD Katsaounis, K Kotsovos, I Gereige, M Abdullah (2022)
  KNN-based ensembles for day-ahead solar power output forecasting, EuroSun, pp. 1755-1766.
  
• I Kakogeorgiou, S Gidaris, B Psomas, Y Avrithis, A Bursuc, K Karantzalos, N Komodakis, What to hide from your students: Attention-guided masked image modeling, European Conference on Computer Vision, 300-318, 2022 (pdf file)
• Kamarianakis,Y., Pantazis, Y., Kalligiannaki, E., Kotsovos, K., Gereige, I., Abdullah, M., Tzavaras, A., Katsaounis,T., Day-ahead forecasting of solar irradiance: KNN-based ensembles, 8th World Conference on Photovoltaic Energy Conversion, 2022. (pdf file)
• Y Kamarianakis, Y Pantazis, E Kalligiannaki, TD Katsaounis, K Kotsovos, ... (2022) Day-Ahead Forecasting of Solar Irradiance & PV Power Output Through Statistical Machine Learning Methods, Saudi Arabia Smart Grid (SASG), 1-5.
  
• Karagiannaki, I., Gourlia, K., Lagani, V., Pantazis, Y., Tsamardinos, I. Learning biologically-interpretable latent representations for gene expression data: Pathway Activity Score Learning Algorithm (2022) Machine Learning, .
• Karaglani, M., Panagopoulou, M., Baltsavia, I., Apalaki, P., Theodosiou, T., Iliopoulos, I., Tsamardinos, I., Chatzaki, E. Tissue‐Specific Methylation Biosignatures for Monitoring Diseases: An In Silico Approach (2022) International Journal of Molecular Sciences, 23 (6), art. no. 2959, .
• M Karaglani, M Panagopoulou, I Baltsavia, P Apalaki, T Theodosiou, I Iliopoulos, I Tsamardinos, E Chatzaki (2022) Tissue-Specific Methylation Biosignatures for Monitoring Diseases: An In Silico Approach, International Journal of Molecular Sciences 23 (6), 2959
  
• Karaglani, M., Panagopoulou, M., Cheimonidi, C., Tsamardinos, I., Maltezos, E., Papanas, N., Papazoglou, D., Mastorakos, G., Chatzaki, E. Liquid Biopsy in Type 2 Diabetes Mellitus Management: Building Specific Biosignatures via Machine Learning (2022) Journal of Clinical Medicine, 11 (4), art. no. 1045,.
• T Katsaounis Y Kamarianakis, Y Pantazis, E Kalligiannaki, K Kotsovos, I Gereige, M Abdullah, A Tzavaras (2022) Day-ahead forecasting of solar irradiance: KNN-based ensembles, 8th World Conference on Photovoltaic Energy Conversion.
  
• T Katsaounis Y Pantazis, E Kalligiannaki, Y Kamarianakis, K Kotsovos, I Gereige, M Abdullah, A Jamal, A Tzavaras, Efficiency evaluation and comparisons of solar cell technologies based on measurements from the Arabian peninsula, EuroSun2022: ISES and IEA SHC International Conference on Solar Energy for Buildings and Industry, 2022
• Kominis, I.K., Loulakis, M. Quantum advantage in biometric authentication with single photons (2022) Journal of Applied Physics, 131 (8), art. no. 084401.
• I Kominis, M Loulakis, Quantum biometric identification of ultrahigh security based on the quantum statistics of photodetection by the human retina, US Patent 11,275,937, 2022 
  
• I Kominis, M Loulakis, ÖE Müstecaplıoglu, Quantum biometrics, Recent Advances in Biometrics 131, 2022
• A Konsta, A Chatzimentor, M Lin, C Dimitriadis, A Kyprioti, M Liu, S Li, A Doxa, A Mazaris (2022) Marine heatwaves threaten key foraging grounds of sea turtles in Southeast Asian Seas, Regional Environmental Change 22 (3), 97
• I Kontoyiannis, L Mertzanis, A Panotopoulou, I Papageorgiou, M Skoularidou (2022) Bayesian context trees: Modelling and exact inference for discrete time series, Journal of the Royal Statistical Society Series B: Statistical Methodology, 84 (4), pp. 1287-1323
• A Kyprioti, A Doxa, V Almpanidou, A Mazaris (2022) Assessing 3-D climatic stability of world’s marine protected areas, https://doi.org/10.21203/rs.3.rs-2025730/v1
• L Lastilla, S Ammirati, D Firmani, N Komodakis, P Merialdo, S Scardapane, Self-supervised learning for medieval handwriting identification: A case study from the Vatican Apostolic Library, Information Processing & Management 59 (3), 102875, 2022
• V Lungu, I Papageorgiou, I Kontoyiannis (2022) Change-point Detection and Segmentation of Discrete Data using Bayesian Context Trees, arXiv preprint arXiv:2203.04341
• V Lungu, I Papageorgiou, I Kontoyiannis (2022) Bayesian change-point detection via context-tree weighting, 2022 IEEE Information Theory Workshop (ITW), 125-130
  
• I Marinescu, S Triantafillou, K Kording, Regression discontinuity threshold optimization, Plos one 17 (11), e0276755, 2022
  
• M Markaki, I Tsamardinos, A Langhammer, V Lagani, K Hveem, OD Roe, A validated clinical risk prediction model for lung cancer in smokers of all ages and exposure types: A HUNT study (vol 31, pg 36, 2018) EBIOMEDICINE 82, 2022
• M Markaki, I Tsamardinos, A Langhammer, V Lagani, K Hveem, OD Røe, Corrigendum to “A validated clinical risk prediction model for lung cancer in smokers of all ages and exposure types: A HUNT study”[EBioMedicine 31 (2018) 36–46], EBioMedicine 82, 2022
• Marshall, J.L., Peshkin, B.N., Yoshino, T., Vowinckel, J., Danielsen, H.E., Melino, G., Tsamardinos, I., Haudenschild, C., Kerr, D.J., Sampaio, C., Rha, S., FitzGerald, K.T., Holland, E.C., Gallagher, D., Garcia-Foncillas, J., Juhl, H. The Essentials of Multiomics (2022) Oncologist, 27 (4), pp. 272-284.
• I Marinescu, S Triantafillou, K Kording (2022) Regression discontinuity threshold optimization, Plos one 17 (11), e0276755
  
• OTD Nguyen, I Fotopoulos, TH Nøst, M Markaki, V Lagani, I Tsamardinos, OD Røe, MA11. 04 Genetic Variants of HUNT Lung Cancer Model Improve Lung Cancer Risk Assessment Over Clinical Models, Journal of Thoracic Oncology 17 (9), S81, 2022.
• Y Pantazis, E Kalligiannaki, Y Kamarianakis, K Kotsovos, I Gereige, M Abdullah, A Jamal, A Tzavaras, T Katsaounis, Efficiency Evaluation and Comparisons of Solar Cell Technologies Based on Measurements from the Arabian Peninsula, 2022.
  
• Pantazis, Y., Paul, D., Fasoulakis, M., Stylianou, Y., Katsoulakis, M.A. Cumulant GAN (2022) IEEE Transactions on Neural Networks and Learning Systems, .
• I Papageorgiou, I Kontoyiannis (2022) The Posterior Distribution of Bayesian Context-Tree Models: Theory and Applications, 2022 IEEE International Symposium on Information Theory (ISIT), 702-707
• P Petsas, A Doxa, V Almpanidou, A Mazaris (2022) Global patterns of sea surface climate connectivity for marine species, Communications Earth & Environment 3 (1), 240
• Petsas P, Doxa A, Almpanidou V, Mazaris AD (2022) Ocean climate connectivity and the future range shifts of marine biodiversity, https://doi.org/10.21203/rs.3.rs-1043050/v1
• Plakandaras, V., Gogas, P., Papadimitriou, T., Tsamardinos, I. Credit Card Fraud Detection with Automated Machine Learning Systems (2022) Applied Artificial Intelligence, 36 (1), art. no. 2086354, 
• OD Røe, I Fotopoulos, OTD Nguyen, TH Nøst, M Markaki, V Lagani, R Mjelle, TM Sandanger, P Sætrom, I Tsamardinos (2022) EP01. 01-009 Common MicroRNAs in Pre-diagnostic Serum Associated with Lung Cancer in Two Cohorts up to Eight Years Before Diagnosis: A HUNT Study, Journal of Thoracic Oncology 17 (9), S164
• V Talisa, F Shah, CC Chang, C Seymour, L Tang, J Kennedy, S Triantafyllou, G Cooper, K DeMerle, F Mayr, D Yealy, A Higgins, S Peake, R Bellomo, D Harrison, P Mouncey, K Rowan, D Angus, S Yende (2022) 1191: HETEROGENEITY IN RESPONSE TO EARLY GOAL-DIRECTED THERAPY IN SEPSIS, Critical Care Medicine 51 (1), 594-594
  
• GV Thomaidis, S Michos, K Papadimitriou, E Chartampilas, I Tsamardinos, Identifying Bipolar patients from controls, using post-mortem cerebellum gene expression data and fully Automated Machine Learning, medRxiv, 2022.01. 22.22269384, 2022
• Tsagris, M., Papadovasilakis, Z., Lakiotaki, K., Tsamardinos, I. The γ-OMP Algorithm for Feature Selection With Application to Gene Expression Data (2022) IEEE/ACM Transactions on Computational Biology and Bioinformatics, 19 (2), pp. 1214-1224.
• Tsamardinos, I. Don't lose samples to estimation (2022) Patterns, 3 (12), art. no. 100612, .
• Tsamardinos, I., Charonyktakis, P., Papoutsoglou, G., Borboudakis, G., Lakiotaki, K., Zenklusen, J.C., Juhl, H., Chatzaki, E., Lagani, V. Just Add Data: automated predictive modeling for knowledge discovery and feature selection (2022) npj Precision Oncology, 6 (1), art. no. 38, .
• Tsourtis, A., Papoutsoglou, G., Pantazis, Y. GAN-Based Training of Semi-Interpretable Generators for Biological Data Interpolation and Augmentation (2022) Applied Sciences (Switzerland), 12 (11), art. no. 5434, .
• A. Tzavaras Y. Kamarianakis, Y. Pantazis, E. Kalligiannaki, K. Kotsovos, I. Gereige, M. Abdullah, Day-Ahead Forecasting of Solar Irradiance: KNN-Based Ensembles, 8th World Conference on Photovoltaic Energy Conversion, 2022
• A. Tzavaras Y. Pantazis, E. Kalligiannaki, Y. Kamarianakis, K. Kotsovos, I. Gereige, M. Abdullah (2022) Performance Evaluation and Comparison of Solar Cell Technologies Based on Historical Data, 39th European Photovoltaic Solar Energy Conference and Exhibition (EUPVSEC2022), 8th World Conference on Photovoltaic Energy Conversion (8th WCPEC) pp. 691-694.

• Agrapetidou, A., Charonyktakis, P., Gogas, P., Papadimitriou, T., Tsamardinos, I. An AutoML application to forecasting bank failures (2021) Applied Economics Letters, 28 (1), pp. 5-9.
• Almpanidou V, Doxa A, Mazaris AD (2021) Combining a cumulative risk index and species distribution data to identify priority areas for marine biodiversity conservation in the Black Sea, Ocean & Coastal Management 213, 105877.
• P Barmpounakis, N Demiris, I Kontoyiannis, G Pavlakis, V Sypsa (2021) Evaluating the effects of vaccine rollout policies in european countries: A simulation study, medRxiv
• TB Berrett, I Kontoyiannis, RJ Samworth (2021) Optimal rates for independence testing via U-statistic permutation tests, The Annals of Statistics 49 (5), 2457-2490
• J Birrell, MA Katsoulakis, Y Pantazis, D Paul, A Tsourtis (2021) A Variance Reduction Method for Neural-based Divergence Estimation
  
• Borboudakis, G., Tsamardinos, I. Extending greedy feature selection algorithms to multiple solutions (2021) Data Mining and Knowledge Discovery, 35 (4), pp. 1393-1434.
• V Borkar, S Chen, A Devraj, I Kontoyiannis, S Meyn (2021) The ODE method for asymptotic statistics in stochastic approximation and reinforcement learning, arXiv preprint arXiv:2110.14427
  
• Chatzimentor A, Almpanidou V, Doxa A, Dimitriadis C, Mazaris AD (2021) Projected redistribution of sea turtle foraging areas reveals important sites for conservation, Climate Change Ecology 2, 100038.
• S Diggavi, A El Gamal, I Kontoyiannis, A Paranjpe, M Subbarao (2021) Joy Thomas: Legacy, Foundation and the IT Society, IEEE BITS the Information Theory Magazine 1 (1), 85-88.
• L Gavalakis, I Kontoyiannis (2021) Entropy and the discrete central limit theorem, arXiv preprint arXiv:2106.00514
• L Gavalakis, I Kontoyiannis (2021) Fundamental limits of lossless data compression with side information, IEEE Transactions on Information Theory 67 (5), 2680-2692
• L Gavalakis, I Kontoyiannis (2021) An information-theoretic proof of a finite de Finetti theorem, Electronic Communications in Probability 26, 1-5
• K Gourlia, M Markaki, C Papadaki, K Rounis, E Vorrias, E Prokova, E Lagoudaki, A Koutsopoulos, I Tsamardinos, D Mavroudis, S Agelaki (2021) MicroRNA Expression Analysis and Biological Pathways in Chemoresistant Non-Small Cell Lung Cancer, MDPI
  
• A Klimova, A Boukhanovsky, A Bilas, V Harmandaris, E Kalligiannaki, E Kanellou (2021) Social Network open data revealing for identification of citizens activities on Urban Environment Objects, TRANSFORMATION 285 (294).
• I Kontoyiannis, YH Lim, K Papakonstantinopoulou, W Szpankowski, Symmetry and the entropy of small-world structures and graphs, 2021 IEEE International Symposium on Information Theory (ISIT), 3026-3031
• I Kontoyiannis, L Tray (2021) Inferring community characteristics in labelled networks, arXiv e-prints, arXiv: 2105.13762
  
• Marcos-Zambrano, L.J., Karaduzovic-Hadziabdic, K., Loncar Turukalo, T., Przymus, P., Trajkovik, V., Aasmets, O., Berland, M., Gruca, A., Hasic, J., Hron, K., Klammsteiner, T., Kolev, M., Lahti, L., Lopes, M.B., Moreno, V., Naskinova, I., Org, E., Paciência, I., Papoutsoglou, G., Shigdel, R., Stres, B., Vilne, B., Yousef, M., Zdravevski, E., Tsamardinos, I., Carrillo de Santa Pau, E., Claesson, M.J., Moreno-Indias, I., Truu, J., Applications of Machine Learning in Human Microbiome Studies: A Review on Feature Selection, Biomarker Identification, Disease Prediction and Treatment (2021) Frontiers in Microbiology, 12, art. no. 634511.
• V Marsocci, S Scardapane, N Komodakis (2021) MARE: Self-supervised multi-attention REsu-Net for semantic segmentation in remote sensing, Remote Sensing 13 (16), 3275
  
• Monnet AC, Cilleros K, Médail F, Albassatneh MC, Arroyo J, Bacchetta G, Bagnoli F, Barina Z, Cartereau M, Casajus N, Dimopoulos P, Domina G, Doxa A, Escudero M, Fady B, Hampe A, Matevski V, Misfud S, Nikolic T, Pavon D, Roig A, Barea ES, Spanu I, Strid A, Vendramin GG, Leriche A (2021) WOODIV, a database of occurrences, functional traits, and phylogenetic data for all Euro-Mediterranean trees, Scientific Data 8, 89. https://doi.org/10.1038/s41597-021-00873-3
  
• Myrtakis, N., Tsamardinos, I., Christophides, V. (2021) PROTEUS: Predictive explanation of anomalies, Proceedings - International Conference on Data Engineering, 2021-April, art. no. 9458931, pp. 1967-1972.
• N Myrtakis, I Tsamardinos, V Christophides (2021) On Predictive Explanation of Data Anomalies, arXiv preprint arXiv:2110.09467
  
• Nissen, L.R., Tsamardinos, I., Eskelund, K., Gradus, J.L., Andersen, S.B., Karstoft, K.-I. Forecasting military mental health in a complete sample of Danish military personnel deployed between 1992-2013 (2021) Journal of Affective Disorders, 288, pp. 167-174.
• Panagopoulou, M., Karaglani, M., Manolopoulos, V.G., Iliopoulos, I., Tsamardinos, I., Chatzaki, E. Deciphering the methylation landscape in breast cancer: Diagnostic and prognostic biosignatures through automated machine learning (2021) Cancers, 13 (7), art. no. 1677, . Planell, N., Lagani, V.,
• Papadogiorgaki, M., Venianaki, M., Charonyktakis, P., Antonakakis, M., Tsamardinos, I., Zervakis, M.E., Sakkalis, V. Heart Rate Classification Using ECG Signal Processing and Machine Learning Methods (2021) BIBE 2021 - 21st IEEE International Conference on BioInformatics and BioEngineering, Proceedings, pp. 1-6.
• I Papageorgiou, I Kontoyiannis (2021) The Bayesian Context Trees State Space Model: Interpretable mixture models for time series, arXiv preprint arXiv:2106.03023
• I Papageorgiou, I Kontoyiannis (2021) Hierarchical Bayesian mixture models for time series using context trees as state space partitions, arXiv preprint arXiv:2106.03023
• I Papageorgiou, I Kontoyiannis, L Mertzanis, A Panotopoulou, ... Revisiting context-tree weighting for Bayesian inference, 2021 IEEE International Symposium on Information Theory (ISIT), 2906-2911.
• A Papapantoleon, P Yanez Sarmiento (2021) Detection of arbitrage opportunities in multi-asset derivatives markets, Dependence Modeling 9 (1), 439-459.
  
• Papoutsoglou, G., Karaglani, M., Lagani, V., Thomson, N., Røe, O.D., Tsamardinos, I., Chatzaki, E. Automated machine learning optimizes and accelerates predictive modeling from COVID-19 high throughput datasets (2021) Scientific Reports, 11 (1), art. no. 15107, .
• Paul, D., Mukherjee, S., Pantazis, Y., Stylianou, Y. A universal multi-speaker multi-style text-to-speech via disentangled representation learning based on Rényi divergence minimization (2021) Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH, 5, pp. 3541-3545.
• N Planell, V Lagani, P Sebastian-Leon, F van der Kloet, E Ewing, N Karathanasis, A Urdangarin, I Arozarena, M Jagodic, I Tsamardinos, S Tarazona, A Conesa, J Tegner, D Gomez-Cabrero (2021) STATegra: multi-omics data integration–a conceptual scheme with a bioinformatics pipeline, Frontiers in genetics 12, 620453
  
• Rounis, K., Makrakis, D., Papadaki, C., Monastirioti, A., Vamvakas, L., Kalbakis, K., Gourlia, K., Xanthopoulos, I., Tsamardinos, I., Mavroudis, D., Agelaki, S. Prediction of outcome in patients with non-small cell lung cancer treated with second line PD-1/PDL-1 inhibitors based on clinical parameters: Results from a prospective, single institution study (2021) PLoS ONE, 16 (6 June), art. no. e0252537, .
• Sebastian-Leon, P., van der Kloet, F., Ewing, E., Karathanasis, N., Urdangarin, A., Arozarena, I., Jagodic, M., Tsamardinos, I., Tarazona, S., Conesa, A., Tegner, J., Gomez-Cabrero, D. STATegra: Multi-Omics Data Integration – A Conceptual Scheme With a Bioinformatics Pipeline (2021) Frontiers in Genetics, 12, art. no. 620453.
• J Taipale, I Kontoyiannis, S Linnarsson (2021)Population-scale testing can suppress the spread of infectious disease, arXiv preprint arXiv:2104.06857
• L Tray, I Kontoyiannis (2021) The feature-first block model, arXiv preprint arXiv:2105.13762
  
• Tsourtis, A., Papoutsoglou, G., Pantazis, Y. (2021) Efficient discrimination between biological populations via neural-based estimation of RÉnyi divergence, UNCECOMP Proceedings, 2021-June.
  

• K Biza, I Tsamardinos, S Triantafillou (2020) Tuning causal discovery algorithms, International Conference on Probabilistic Graphical Models, 17-28
  
• Chatzaki, E., Tsamardinos, I. Somatic copy number aberrations detected in circulating tumor DNA can hold diagnostic value for early detection of hepatocellular carcinoma (2020) EBioMedicine, 57, art. no. 102851, .
• G Chatzinikolaou, K Stratigi, K Agathangelou, M Tsekrekou, E Goulielmaki, O Chatzidoukaki, K Gkirtzimanaki, T Aid-Pavlidis, M Aivaliotis, P Pavlidis, I Tsamardinos, P Topalis, BBouwman, N Crosetto, J Altmüller, G Garinis (2020) ERCC1-XPF Interacts with Topoisomerase IIβ to Facilitate the Repair of Activity-induced DNA Breaks, bioRxiv, 2020.01. 03.892703
  
• A Chazirakis, V Kirieri, IM Sarris, E Kalligiannaki, V Harmandaris (2020) Neural Network Potential Surfaces: A Comparison of two Approaches, Procedia Computer Science 178, 345-354.
  
• Cheliotis, D., Kontoyiannis, I., Loulakis, M., Toumpis, S. A simple network of nodes moving on the circle (2020) Random Structures and Algorithms, 57 (2), pp. 317-338.
  
• Cho, N., El Asmar, M., Underwood, S., Kamarianakis, Y.,  Long-Term Performance Benefits of the Design-Build Delivery Method Applied to Road Pavement Projects in the U.S. (2020) KSCE Journal of Civil Engineering, 24 (4), pp. 1049-1059.
• AM Devraj, I Kontoyiannis, SP Meyn (2020) Differential temporal difference learning, IEEE Transactions on Automatic Control 66 (10), 4652-4667
• A Devraj, I Kontoyiannis, S Meyn (2020) Geometric ergodicity in a weighted Sobolev space
• Doxa A, Devictor V, Baumel A, Pavon D, Medail F, Leriche A (2020) Beyond taxonomic diversity: Revealing spatial mismatches in phylogenetic and functional diversity facets in Mediterranean tree communities in southern France, Forest Ecology and Management 474, 118318.
• Doxa A, Prastacos P (2020) Using Rao's quadratic entropy to define environmental heterogeneity priority areas in the European Mediterranean biome, Biological Conservation 241, 108366.
  
• Dupuis, P., Katsoulakis, M.A., Pantazis, Y., Rey-Bellet, L., (2020) Sensitivity analysis for rare events based on rényi divergence (2020) Annals of Applied Probability, 30 (4), pp. 1507-1533.
• S Fafalios, P Charonyktakis, I Tsamardinos (2020) Gradient Boosting Trees, Gnosis Data Analysis PC, 1-3
  
• L Gavalakis, I Kontoyiannis (2020) Sharp Second-Order Pointwise Asymptotics for Lossless Compression with Side Information, Entropy 22 (6), 705
• L Gavalakis, I Kontoyiannis, Lossless Data Compression with Side Information: Nonasymptotics and Dispersion, 2020 IEEE International Symposium on Information Theory (ISIT), 2179-2183
• R Cavallari, S Toumpis, R Verdone, I Kontoyiannis (2020) Packet speed and cost in mobile wireless delay-tolerant networks, IEEE Transactions on Information Theory 66 (9), 5683-5702
  
• Giacomazzo, M., Kamarianakis, Y., Bayesian estimation of subset threshold autoregressions: short-term forecasting of traffic occupancy (2020) Journal of Applied Statistics, 47 (13-15), pp. 2658-2689.
• D Gomez-Cabrero, S Tarazona, I Ferreirós-Vidal, RN Ramirez, A Schmidt, T Reijmers, V Von Saint Paul, F Marabita, J Rodríguez-Ubreva, A Garcia-Gomez, T Carroll, L Cooper, Z Liang, G Dharmalingam, F van der Kloet, A Harms, L Balzano-Nogueira, V Lagani, I Tsamardinos, M Lappe, D Maier, J Westerhuis, T Hankemeier, A Imhof, E Ballestar, A Mortazavi, M Merkenschlager, J Tegner, A Conesa (2020) Metadata record for: STATegra, a comprehensive multi-omics dataset of B-cell differentiation in mouse, figshare
  
• T Jin, A Chazirakis, E Kalligiannaki, V Harmandaris, MA Katsoulakis (2020) Data-driven uncertainty quantification for systematic coarse-grained models, Soft Materials 18 (2-3), 348-368.
  
• Karagiannaki, I., Pantazis, Y., Chatzaki, E., Tsamardinos, I., Pathway Activity Score Learning for Dimensionality Reduction of Gene Expression Data (2020) Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 12323 LNAI, pp. 246-261.
• I Karagiannaki, Y Pantazis, E Chatzaki, I Tsamardinos (2020) Pathway activity score learning for dimensionality reduction of gene expression data, Discovery Science: 23rd International Conference, DS 2020, Thessaloniki, Greece, October 19–21, 2020, Proceedings 23, pp. 246-261
• Karaglani, M., Gourlia, K., Tsamardinos, I., Chatzaki, E. Accurate blood-based diagnostic biosignatures for alzheimer’s disease via automated machine learning (2020) Journal of Clinical Medicine, 9 (9), art. no. 3016, pp. 1-14.
• Karstoft, K.-I., Tsamardinos, I., Eskelund, K., Andersen, S.B., Nissen, L.R,. Applicability of an automated model and parameter selection in the prediction of screening-level PTSD in Danish soldiers following deployment: Development study of transferable predictive models using automated machine learning (2020) JMIR Medical Informatics, 8 (7), art. no. e17119, .
• I Kontoyiannis, YH Lim, K Papakonstantinopoulou, W Szpankowski (2020) Compression and symmetry of small-world graphs and structures, arXiv preprint arXiv:2007.15981
  
• Malliaraki, N., Lakiotaki, K., Vamvoukaki, R., Notas, G., Tsamardinos, I., Kampa, M., Castanas, E. Translating vitamin D transcriptomics to clinical evidence: Analysis of data in asthma and chronic obstructive pulmonary disease, followed by clinical data meta-analysis (2020) Journal of Steroid Biochemistry and Molecular Biology, 197, art. no. 105505, .
• Nikoloudakis, N., Stagakis, S., Mitraka, Z., Kamarianakis, Y., Chrysoulakis, N. Spatial interpolation of urban air temperatures using satellite-derived predictors (2020) Theoretical and Applied Climatology, 141 (1-2), pp. 657-672.
• Pantazis, Y., Tselas, C., Lakiotaki, K., Lagani, V., Tsamardinos, I. Latent Feature Representations for Human Gene Expression Data Improve Phenotypic Predictions (2020) Proceedings - 2020 IEEE International Conference on Bioinformatics and Biomedicine, BIBM 2020, art. no. 9313286, pp. 2505-2512.
• Paul, D., Shifas, M.P.V., Pantazis, Y., Stylianou, Y. Enhancing speech intelligibility in text-to-speech synthesis using speaking style conversion (2020) Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH, 2020-October, pp. 1361-1365.
• Paul, D., Pantazis, Y., Stylianou, Y. (2020) Speaker conditional WaveRNN: Towards universal neural vocoder for unseen speaker and recording conditions, Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH, 2020-October, pp. 235-239.
• D Paul, MPV Shifas, Y Pantazis, Y Stylianou (2020) Enhancing Speech Intelligibility in Text-To-Speech Synthesis using Speaking Style Conversion, INTERSPEECH, 1361-1365
• M Riabiz, T Ardeshiri, I Kontoyiannis, S Godsill (2020) Nonasymptotic Gaussian approximation for inference with stable noise, IEEE Transactions on Information Theory 66 (8), 4966-4991.
• OD Røe, M Markaki, I Tsamardinos, V Lagani, OTD Nguyen, JH Pedersen, Z Saghir, HG Ashraf (2020) ‘Reduced’ HUNT model outperforms NLST and NELSON study criteria in predicting lung cancer in the Danish screening trial, BMJ open respiratory research 6 (1), e000512
  
• Simantiraki, O., Cooke, M., Pantazis, Y., Effects of Spectral Tilt on Listeners' Preferences and Intelligibility (2020) ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing - Proceedings, 2020-May, art. no. 9054117, pp. 6254-6258.
• M Tsagris, Z Papadovasilakis, K Lakiotaki, I Tsamardinos (2020) The gamma-OMP Algorithm for Feature Selection With Application to Gene Expression Data, IEEE/ACM Transactions on Computational Biology and Bioinformatics 19 (2), 1214-1224.
• Tsamardinos, I., Fanourgakis, G.S., Greasidou, E., Klontzas, E., Gkagkas, K., Froudakis, G.E. An Automated Machine Learning architecture for the accelerated prediction of Metal-Organic Frameworks performance in energy and environmental applications (2020) Microporous and Mesoporous Materials, 300, art. no. 110160.
• A Tsourtis, Y Pantazis, I Tsamardinos (2020) Inference of Stochastic Dynamical Systems from Cross-Sectional Population Data, arXiv preprint arXiv:2012.05055
  
• Velli, M.-C., Tsibidis, G.D., Mimidis, A., Skoulas, E., Pantazis, Y., Stratakis, E. Predictive modeling approaches in laser-based material processing (2020) Journal of Applied Physics, 128 (18), art. no. 018235.
• Vernardos, G., Tsagkatakis, G., Pantazis, Y., Quantifying the structure of strong gravitational lens potentials with uncertainty-aware deep neural networks (2020) Monthly Notices of the Royal Astronomical Society, 499 (4), pp. 5641-5652.
• Verrou, K.-M., Tsamardinos, I., Papoutsoglou, G. Learning Pathway Dynamics from Single-Cell Proteomic Data: A Comparative Study (2020) Cytometry Part A, 97 (3), pp. 241-252.
• Xanthopoulos, I., Tsamardinos, I., Christophides, V., Simon, E., Salinger, A. Putting the human back in the AutoML loop (2020) EDBT/ICDT Workshops, CEUR Workshop Proceedings, 2578.
  

• Adamou, M., Antoniou, G., Greasidou, E., Lagani, V., Charonyktakis, P., Tsamardinos, I., Doyle, M. Toward Automatic Risk Assessment to Support Suicide Prevention (2019) Crisis, 40 (4), pp. 249-256.
• N Adiga, Y Pantazis, V Tsiaras, Y Stylianou (2019) Speech Enhancement for Noise-Robust Speech Synthesis Using Wasserstein GAN, INTERSPEECH, 1821-1825
  
• T Asvestopoulou, V Manousaki, A Psistakis, E Nikolli, V Andreadakis, IM Aslanides, Y Pantazis, I Smyrnakis, M Papadopouli, Towards a robust and accurate screening tool for dyslexia with data augmentation using GANs, 2019 IEEE 19th International Conference on Bioinformatics and Bioengineering (BIBE) pp. 775-782
  
• G Baxevani, E Kalligiannaki, V Harmandaris (2019) Study of the transient dynamics of coarse-grained molecular systems with the path-space force-matching method, Procedia Computer Science 156, 59-68.
  
• Borboudakis and I. Tsamardinos (2019) Forward-backward selection with early dropping. The Journal of Machine Learning Research, 20 (1), 276-314.
• A.J. Brazel, Y. Kamarianakis, X. Li, B.L. Turner (2019) On the effects of landscape configuration on summer diurnal temperatures in urban residential areas: application in Phoenix, AZ, Frontiers of Earth Science, Vol. 13 (3), pp. 445-463.
  
• Ewing, E., Kular, L., Fernandes, S.J., Karathanasis, N., Lagani, V., Ruhrmann, S., Tsamardinos, I., Tegner, J., Piehl, F., Gomez-Cabrero, D., Jagodic, M. Combining evidence from four immune cell types identifies DNA methylation patterns that implicate functionally distinct pathways during Multiple Sclerosis progression (2019) EBioMedicine, 43, pp. 411-423.
• Fernandes, S.J., Morikawa, H., Ewing, E., Ruhrmann, S., Joshi, R.N., Lagani, V., Karathanasis, N., Khademi, M., Planell, N., Schmidt, A., Tsamardinos, I., Olsson, T., Piehl, F., Kockum, I., Jagodic, M., Tegnér, J., Gomez-Cabrero, D. Non-parametric combination analysis of multiple data types enables detection of novel regulatory mechanisms in T cells of multiple sclerosis patients (2019) Scientific Reports, 9 (1), art. no. 11996.
• Ferreirós-Vidal, I., Carroll, T., Zhang, T., Lagani, V., Ramirez, R.N., Ing-Simmons, E., Gómez-Valadés, A.G., Cooper, L., Liang, Z., Papoutsoglou, G., Dharmalingam, G., Guo, Y., Tarazona, S., Fernandes, S.J., Noori, P., Silberberg, G., Fisher, A.G., Tsamardinos, I., Mortazavi, A., Lenhard, B., Conesa, A., Tegner, J., Merkenschlager, M., Gomez-Cabrero, D. Feedforward regulation of Myc coordinates lineage-specific with housekeeping gene expression during B cell progenitor cell differentiation (2019) PLoS Biology, 17 (4), art. no. e2006506.
• S Godsill, M Riabiz, I Kontoyiannis (2019) The Lévy state space model, 2019 53rd Asilomar Conference on Signals, Systems, and Computers, 487-494
• Gomez-Cabrero, D., Tarazona, S., Ferreirós-Vidal, I., Ramirez, R.N., Company, C., Schmidt, A., Reijmers, T., Paul, V.S., Marabita, F., Rodríguez-Ubreva, J., Garcia-Gomez, A., Carroll, T., Cooper, L., Liang, Z., Dharmalingam, G., van der Kloet, F., Harms, A.C., Balzano-Nogueira, L., Lagani, V., Tsamardinos, I., Lappe, M., Maier, D., Westerhuis, J.A., Hankemeier, T., Imhof, A., Ballestar, E., Mortazavi, A., Merkenschlager, M., Tegner, J., Conesa, A. STATegra, a comprehensive multi-omics dataset of B-cell differentiation in mouse (2019) Scientific Data, 6 (1), art. no. 256.
• V Harmandaris, E Kalligiannaki, M Katsoulakis (2019) Systematic Coarse-Grained Models for Molecular Systems Using Entropy, Proceedings of 5th International Electronic Conference on Entropy and Its Applications
  doi:10.3390/ecea-5-06710
  
• E Kalligiannaki, V Harmandaris, M Katsoulakis (2019) Systematic Coarse-Grained Models for Molecular Systems Using Entropy, Proceedings 60 (1), 27.
• GT Kossioris, M Loulakis, PE Souganidis (2019) The deterministic and stochastic shallow lake problem, Probability and Analysis in Interacting Physical Systems: In Honor of SRS Varadhan, pp. 49-74
• Kyriakis, D., Kanterakis, A., Manousaki, T., Tsakogiannis, A., Tsagris, M., Tsamardinos, I., Papaharisis, L., Chatziplis, D., Potamias, G., Tsigenopoulos, C.S. Scanning of genetic variants and genetic mapping of phenotypic traits in gilthead seabream through ddRAD sequencing (2019) Frontiers in Genetics, 10 (JUN), art. no. 675.
• Lakiotaki, K., Georgakopoulos, G., Castanas, E., Røe, O.D., Borboudakis, G., Tsamardinos, I., A data driven approach reveals disease similarity on a molecular level (2019) npj Systems Biology and Applications, 5 (1), art. no. 39.
• Loos, M.S., Ramakrishnan, R., Vranken, W., Tsirigotaki, A., Tsare, E.-P., Zorzini, V., De Geyter, J., Yuan, B., Tsamardinos, I., Klappa, M., Schymkowitz, J., Rousseau, F., Karamanou, S., Economou, A. Structural basis of the subcellular topology landscape of Escherichia coli (2019) Frontiers in Microbiology, 10, art. no. 1670, pp. 1-22.
• M Loulakis, MG Stamatakis (2019) Generalized Young measures and the hydrodynamic limit of condensing zero range processes, arXiv preprint arXiv:1910.00493
• T Lux, A Papapantoleon (2019) Model-free bounds on Value-at-Risk using extreme value information and statistical distances. Insurance: Mathematics and Economics 86, 73-83.
  
• K Mouloudakis, M Loulakis, IK Kominis (2019) Quantum trajectories in spin-exchange collisions reveal the nature of spin-noise correlations in multispecies alkali-metal vapors, Physical Review Research 1 (3), 033017
• OT Nguyen, M Markaki, A Sharma, C Chatzipantsiou, V Lagani, I Tsamardinos, O Røe (2019) P1. 11-13 Mass spectrometry proteomics analysis discovers biomarkers in serum months to years before non-small cell lung cancer: the HUNT study, Journal of Thoracic Oncology 14 (10), S520
• OTD Nguyen, M Markaki, C Chatzipantsiou, A Sharma, V Lagani, I Tsamardinos, OD Røe (2019) Proteomics analysis discovers biomarkers in serum months to years before small cell lung cancer: The HUNT study. Journal of Clinical Oncology 37 (15_suppl), e20095-e20095
  
• Panagopoulou, M., Karaglani, M., Balgkouranidou, I., Biziota, E., Koukaki, T., Karamitrousis, E., Nena, E., Tsamardinos, I., Kolios, G., Lianidou, E., Kakolyris, S., Chatzaki, E. Circulating cell-free DNA in breast cancer: size profiling, levels, and methylation patterns lead to prognostic and predictive classifiers (2019) Oncogene, 38 (18), pp. 3387-3401.
• Y Pantazis, D Paul, M Fasoulakis, Y Stylianou (2019) Training Generative Adversarial Networks with Weights, 27th European Signal Processing Conference, EUSIPCO 2019.
  
• Pantazis, Y., Tsamardinos, I. (2019) A unified approach for sparse dynamical system inference from temporal measurements, Bioinformatics, 35 (18), pp. 3387-3396.
• Y. Pantazis, M. Tsagris and A.T.A. Wood (2019) Gaussian Asymptotic Limits for the α-transformation in the Analysis of Compositional Data. Sankhya A, 1-20.
• Y Pantazis, I Tsamardinos (2019) A unified approach for sparse dynamical system inference from temporal measurements, Bioinformatics, btz065
  
• Y Pantazis, V Tsiaras, Y Stylianou (2019) Connections between Reassigned Spectrum and Least Squares Estimation for Sinusoidal Models, 27th European Signal Processing Conference, EUSIPCO 2019
• A Papapantoleon, D Possamai, A Saplaouras (2019) Stability results for martingale representations: the general case, Transactions of the American Mathematical Society 372 (8), 5891-5946
  
• G Papavieros, I Kontoyiannis, V Constantoudis, E Gogolides (2019) Denoising line edge roughness measurement using hidden Markov models, Metrology, Inspection, and Process Control for Microlithography XXXIII, Vol. 10959, pp. 656-663.
• Papoutsoglou, G., Lagani, V., Schmidt, A., Tsirlis, K., Cabrero, D.-G., Tegnér, J., Tsamardinos, I., Challenges in the Multivariate Analysis of Mass Cytometry Data: The Effect of Randomization (2019) Cytometry Part A, 95 (11), pp. 1178-1190.
• D Paul, Y Pantazis, Y Stylianou (2019) Non-Parallel Voice Conversion Using Weighted Generative Adversarial Networks, Interspeech, 659-663
• D Paul, Y Pantazis, Y Stylianou (2019) Weighted generative adversarial network for many-to-many voice conversion, Universitätsbibliothek der RWTH Aachen
  
• Røe, O.D., Markaki, M., Tsamardinos, I., Lagani, V., Nguyen, O.T.D., Pedersen, J.H., Saghir, Z., Ashraf, H.G. 'Reduced' HUNT model outperforms NLST and NELSON study criteria in predicting lung cancer in the Danish screening trial (2019) BMJ Open Respiratory Research, 6 (1), art. no. e000512, .
• OD Røe, OTD Nguyen, K Lakiotaki, I Tsamardinos, V Lagani, M Markaki (2019) Improvement of lung cancer risk prediction adding SNPs to the HUNT Lung Cancer Model: A HUNT Study. Journal of Clinical Oncology 37 (15_suppl), e20696-e20696
  
• Tsagris, M., Tsamardinos, I., Feature selection with the R package MXM (2019) F1000Research, 7, art. no. 1505.
• Tsamardinos, I., Borboudakis, G., Katsogridakis, P., Pratikakis, P., Christophides, V. A greedy feature selection algorithm for Big Data of high dimensionality (2019) Machine Learning, 108 (2), pp. 149-202.
• M. Wang, Y. Kamarianakis, M. Georgescu, M. Moustaoui (2019) Spatio-Temporal Modeling for Regional Climate Model Evaluation: Eigenvector Filtering Versus Bayesian CAR, 99th American Meteorological Society Annual Meeting.
  
• B. Wang, Y. Zheng, D. Fang, Y. Kamarianakis and J. Wilson (2019) Split bootstrap hierarchical modeling of antibiotics abuse in China. Statistics in Medicine, 38, 2282-2291.